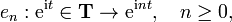Fredholm Operator - Examples

Examples

Let H be a Hilbert space with an orthonormal basis {en} indexed by the non negative integers. The (right) shift operator S on H is defined by

This operator S is injective (actually, isometric) and has a closed range of codimension 1, hence S is Fredholm with ind(S) = −1. The powers Sk, k ≥ 0, are Fredholm with index −k. The adjoint S∗ is the left shift,

The left shift S∗ is Fredholm with index 1.

If H is the classical Hardy space H2(T) on the unit circle T in the complex plane, then the shift operator with respect to the orthonormal basis of complex exponentials

e_n : \mathrm{e}^{\mathrm{i} t} \in \mathbf{T} \rightarrow \mathrm{e}^{\mathrm{i} n t}, \quad n \ge 0, \,

is the multiplication operator Mφ with the function φ = e1. More generally, let φ be a complex continuous function on T that does not vanish on T, and let Tφ denote the Toeplitz operator with symbol φ, equal to multiplication by φ followed by the orthogonal projection P from L2(T) onto H2(T):

Then Tφ is a Fredholm operator on H2(T), with index related to the winding number around 0 of the closed path t ∈ → φ(e i t ) : the index of Tφ, as defined in this article, is the opposite of this winding number.

Read more about this topic:  Fredholm Operator

Famous quotes containing the word examples:

    “There are many examples of women that have excelled in learning, and even in war, but this is no reason we should bring ‘em all up to Latin and Greek or else military discipline, instead of needle-work and housewifry.”
    —Bernard Mandeville (1670–1733)

    “No rules exist, and examples are simply life-savers answering the appeals of rules making vain attempts to exist.”
    —André Breton (1896–1966)

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)