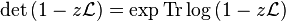Fredholm Kernel - Grothendieck's Theorem

Grothendieck's Theorem

If is an operator of order then a trace may be defined, with

where are the eigenvalues of . Furthermore, the Fredholm determinant

$\det \left( 1-z\mathcal{L}\right)= \prod_i \left(1-\rho_i z \right)$

is an entire function of z. The formula

$\det \left( 1-z\mathcal{L}\right)= \exp \mbox{Tr} \log\left( 1-z\mathcal{L}\right)$

holds as well. Finally, if is parameterized by some complex-valued parameter w, that is, and the parameterization is holomorphic on some domain, then

is holomorphic on the same domain.

Read more about this topic: Fredholm Kernel

“To insure the adoration of a theorem for any length of time, faith is not enough, a police force is needed as well.”
—Albert Camus (1913–1960)