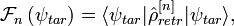Fidelity of Quantum Measurements
The fidelity of a measurement with a projective measurement is defined as the overlap between their pre-measurement states:
where and are respectively the pre-measurement state corresponding to the result "n" and the target state in which we would like measuring the system before its interaction with the measurement apparatus.
The pre-measurement state is the main tool of the retrodictive approach of quantum physics in which we make predictions about state preparations leading to a certain measurement result. In such an approach, this fidelity has an interesting meaning: this is nothing else than the retrodictive probability of preparing the system in the target state when we read the result "n". Thus, when a measurement is sufficiently faithful, the most probable state in which the system was prepared before the measurement giving the result "n" is this target state .
Read more about this topic: Fidelity Of Quantum States
Famous quotes containing the words fidelity and/or quantum:
“Total loyalty is possible only when fidelity is emptied of all concrete content, from which changes of mind might naturally arise.”
—Hannah Arendt (1906–1975)
“But how is one to make a scientist understand that there is something unalterably deranged about differential calculus, quantum theory, or the obscene and so inanely liturgical ordeals of the precession of the equinoxes.”
—Antonin Artaud (1896–1948)