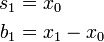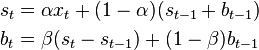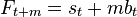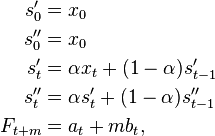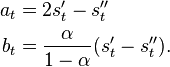Exponential Smoothing - Double Exponential Smoothing

Double Exponential Smoothing

Simple exponential smoothing does not do well when there is a trend in the data. In such situations, several methods were devised under the name "double exponential smoothing".

One method, sometimes referred to as "Holt-Winters double exponential smoothing" works as follows:

Again, the raw data sequence of observations is represented by {xt}, beginning at time t = 0. We use {st} to represent the smoothed value for time t, and {bt} is our best estimate of the trend at time t. The output of the algorithm is now written as Ft+m, an estimate of the value of x at time t+m, m>0 based on the raw data up to time t. Double exponential smoothing is given by the formulas

\begin{align} s_1& = x_0\\ b_1& = x_1 - x_0\\ \end{align}

And for t > 1 by

\begin{align} s_{t}& = \alpha x_{t} + (1-\alpha)(s_{t-1} + b_{t-1})\\ b_{t}& = \beta (s_t - s_{t-1}) + (1-\beta)b_{t-1}\\ \end{align}

where α is the data smoothing factor, 0 < α < 1, and β is the trend smoothing factor, 0 < β < 1.

To forecast beyond x_t

\begin{align} F_{t+m}& = s_t + mb_t \end{align}

Setting the initial value b0 is a matter of preference. An option other than the one listed above is (xn - x0)/n for some n > 1.

Note that F0 is undefined (there is no estimation for time 0), and according to the definition F1=s0+b0, which is well defined, thus further values can be evaluated.

A second method, referred to as either Brown's linear exponential smoothing (LES) or Brown's double exponential smoothing works as follows.

\begin{align} s'_0& = x_0\\ s''_0& = x_0\\ s'_{t}& = \alpha x_{t} + (1-\alpha)s'_{t-1}\\ s''_{t}& = \alpha s'_{t} + (1-\alpha)s''_{t-1}\\ F_{t+m}& = a_t + mb_t, \end{align}

where at, the estimated level at time t and bt, the estimated trend at time t are:

\begin{align} a_t& = 2s'_t - s''_t\\ b_t& = \frac \alpha {1-\alpha} (s'_t - s''_t). \end{align}

Read more about this topic:  Exponential Smoothing

Famous quotes containing the words double and/or smoothing:

    “since I see
    Your double heart,
    Farewell my part!”
    —Sir Thomas Wyatt (1503?–1542)

    “Generation on generation, your neck rubbed the windowsill
    of the stall, smoothing the wood as the sea smooths glass.”
    —Donald Hall (b. 1928)