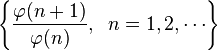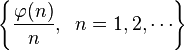Euler's Totient Function - Ratio of Consecutive Values

Ratio of Consecutive Values

In 1950 Somayajulu proved

$\lim\inf \frac{\varphi(n+1)}{\varphi(n)}= 0$ and $\lim\sup \frac{\varphi(n+1)}{\varphi(n)}= \infty.$

In 1954 Schinzel and Sierpiński strengthened this, proving that the set

$\left\{\frac{\varphi(n+1)}{\varphi(n)},\;\;n = 1,2,\cdots\right\}$

is dense in the positive real numbers. They also proved that the set

$\left\{\frac{\varphi(n)}{n},\;\;n = 1,2,\cdots\right\}$

is dense in the interval (0, 1).

Read more about this topic: Euler's Totient Function

Famous quotes containing the words ratio of, ratio and/or values:

“Personal rights, universally the same, demand a government framed on the ratio of the census: property demands a government framed on the ratio of owners and of owning.”
—Ralph Waldo Emerson (1803–1882)

“Official dignity tends to increase in inverse ratio to the importance of the country in which the office is held.”
—Aldous Huxley (1894–1963)

“Tallulah [Bankhead] was the foremost naughty girl of her era but, in those days, “naughty” meant piquant, whereas values have so changed that now, in the 1970s, it generally means nauseating.”
—Anita Loos (1888–1981)