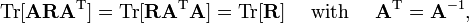Equivalence Classes
It is of interest to remark that the trace (sum of diagonal elements) of the real rotation matrix given above is 1 + 2cosφ. Since a trace is invariant under an orthogonal matrix transformation:
it follows that all matrices that are equivalent to R by an orthogonal matrix transformation have the same trace. The matrix transformation is clearly an equivalence relation, that is, all equivalent matrices form an equivalence class. In fact, all proper rotation 3×3 rotation matrices form a group, usually denoted by SO(3) (the special orthogonal group in 3 dimensions) and all matrices with the same trace form an equivalence class in this group. Elements of such an equivalence class share their rotation angle, but all rotations are around different axes. If n is an eigenvector of R with eigenvalue 1, then An is an eigenvector of ARAT, also with eigenvalue 1. Unless A = E, n and An are different.
Read more about this topic: Euler's Rotation Theorem
Famous quotes containing the word classes:
“Intellectuals can tell themselves anything, sell themselves any bill of goods, which is why they were so often patsies for the ruling classes in nineteenth-century France and England, or twentieth-century Russia and America.”
—Lillian Hellman (1907–1984)