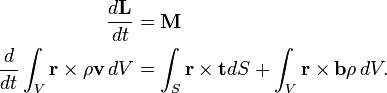Euler's Laws of Motion - Explanation and Derivation

Explanation and Derivation

The density of internal forces at every point in a deformable body are not necessarily equal, i.e. there is a distribution of stresses throughout the body. This variation of internal forces throughout the body is governed by Newton's second law of motion of conservation of linear momentum and angular momentum, which normally are applied to a mass particle but are extended in continuum mechanics to a body of continuously distributed mass. For continuous bodies these laws are called Euler’s laws of motion. If a body is represented as an assemblage of discrete particles, each governed by Newton’s laws of motion, then Euler’s equations can be derived from Newton’s laws. Euler’s equations can, however, be taken as axioms describing the laws of motion for extended bodies, independently of any particle structure.

The total body force applied to a continuous body with mass m, mass density ρ, and volume V, is the volume integral integrated over the volume of the body:

where b is the force acting on the body per unit mass (dimensions of acceleration, misleadingly called the "body force"), and dm = ρdV is an infinitesimal mass element of the body.

Body forces and contact forces acting on the body lead to corresponding moments of force (torques) relative to a given point. Thus, the total applied torque M about the origin is given by

where M_B and M_C respectively indicate the moments caused by the body and contact forces.

Thus, the sum of all applied forces and torques (with respect to the origin of the coordinate system) in the body can be given as the sum of a volume and surface integral:

where t = t(n) is called the surface traction, integrated over the surface of the body, in turn n denotes a unit vector normal and directed outwards to the surface S.

Let the coordinate system (x₁, x₂, x₃) be an inertial frame of reference, r be the position vector of a point particle in the continuous body with respect to the origin of the coordinate system, and v = dr/dt be the velocity vector of that point.

Euler’s first axiom or law (law of balance of linear momentum or balance of forces) states that in an inertial frame the time rate of change of linear momentum p of an arbitrary portion of a continuous body is equal to the total applied force F acting on the considered portion, and it is expressed as

$\begin{align} \frac{d\mathbf p}{dt} &= \mathbf F \\ \frac{d}{dt}\int_V \rho\mathbf v\,dV&=\int_S \mathbf t dS + \int_V \mathbf b\rho \,dV. \\ \end{align}$

Euler’s second axiom or law (law of balance of angular momentum or balance of torques) states that in an inertial frame the time rate of change of angular momentum L of an arbitrary portion of a continuous body is equal to the total applied torque M acting on the considered portion, and it is expressed as

$\begin{align} \frac{d\mathbf L}{dt} &= \mathbf M \\ \frac{d}{dt}\int_V \mathbf r\times\rho\mathbf v\,dV&=\int_S \mathbf r \times \mathbf t dS + \int_V \mathbf r \times \mathbf b\rho\,dV. \\\end{align}$

The derivatives of p and L are material derivatives.

Read more about this topic: Euler's Laws Of Motion

Famous quotes containing the word explanation:

“Are cans constitutionally iffy? Whenever, that is, we say that we can do something, or could do something, or could have done something, is there an if in the offing—suppressed, it may be, but due nevertheless to appear when we set out our sentence in full or when we give an explanation of its meaning?”
—J.L. (John Langshaw)