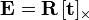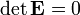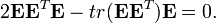Properties of The Essential Matrix
Not every arbitrary matrix can be an essential matrix for some stereo cameras. To see this notice that it is defined as the matrix product of one rotation matrix and one skew-symmetric matrix, both . The skew-symmetric matrix must have two singular values which are equal and another which is zero. The multiplication of the rotation matrix does not change the singular values which means that also the essential matrix has two singular values which are equal and one which is zero. The properties described here are sometimes referred to as internal constraints of the essential matrix.
If the essential matrix is multiplied by a non-zero scalar, the result is again an essential matrix which defines exactly the same constraint as does. This means that can be seen as an element of a projective space, that is, two such matrices are considered equivalent if one is a non-zero scalar multiplication of the other. This is a relevant position, for example, if is estimated from image data. However, it is also possible to take the position that is defined as
and then has a well-defined "scaling". It depends on the application which position is the more relevant.
The constraints can also be expressed as
and
Here the last equation is matrix constraint, which can be seen as 9 constraints, one for each matrix element. These constraints are often used for determining the essential matrix from five corresponding point pairs.
The essential matrix has five or six degrees of freedom, depending on whether or not it is seen as a projective element. The rotation matrix and the translation vector have three degrees of freedom each, in total six. If the essential matrix is considered as a projective element, however, one degree of freedom related to scalar multiplication must be subtracted leaving five degrees of freedom in total.
Read more about this topic: Essential Matrix
Famous quotes containing the words properties of the, properties of, properties, essential and/or matrix:
“A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
—Ralph Waldo Emerson (1803–1882)
“A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
—Ralph Waldo Emerson (1803–1882)
“A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
—Ralph Waldo Emerson (1803–1882)
“And he gave it for his opinion, that whoever could make two ears of corn, or two blades of grass, to grow upon a spot of ground where only one grew before, would deserve better of mankind, and do more essential service to his country, than the whole race of politicians put together.”
—Jonathan Swift (1667–1745)
““The matrix is God?”
“In a manner of speaking, although it would be more accurate ... to say that the matrix has a God, since this being’s omniscience and omnipotence are assumed to be limited to the matrix.”
“If it has limits, it isn’t omnipotent.”
“Exactly.... Cyberspace exists, insofar as it can be said to exist, by virtue of human agency.””
—William Gibson (b. 1948)