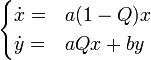Error Catastrophe - Basic Mathematical Model

Basic Mathematical Model

Consider a virus which has a genetic identity modeled by a string of ones and zeros (e.g. 11010001011101....). Suppose that the string has fixed length L and that during replication the virus copies each digit one by one, making a mistake with probability q independently of all other digits.

Due to the mutations resulting from erroneous replication, there exist up to 2L distinct strains derived from the parent virus. Let x_i denote the concentration of strain i; let a_i denote the rate at which strain i reproduces; and let Q_ij denote the probability of a virus of strain i mutating to strain j.

Then the rate of change of concentration x_j is given by

At this point, we make a mathematical idealisation: we pick the fittest strain (the one with the greatest reproduction rate a_j) and assume that it is unique (i.e. that the chosen a_j satisfies a_j > a_i for all i); and we then group the remaining strains into a single group. Let the concentrations of the two groups be x, y with reproduction rates a>b, respectively; let Q be the probability of a virus in the first group (x) mutating to a member of the second group (y) and let R be the probability of a member of the second group returning to the first (via an unlikely and very specific mutation). The equations governing the development of the populations are:

$\begin{cases} \dot{x} = & a(1-Q)x + bRy \\ \dot{y} = & aQx + b(1-R)y \\ \end{cases}$

We are particularly interested in the case where L is very large, so we may safely neglect R and instead consider:

$\begin{cases} \dot{x} = & a(1-Q)x \\ \dot{y} = & aQx + by \\ \end{cases}$

Then setting z = x/y we have

$\begin{matrix} \frac{\partial z}{\partial t} & = & \frac{\dot{x} y - x \dot{y}}{y^2} \\ && \\ & = & \frac{a(1-Q)xy - x (aQx + by)}{y^2} \\ && \\ & = & a(1-Q)z - (aQz^2 +bz) \\ && \\ & = & z(a(1-Q) -aQz -b) \\ \end{matrix}$ .

Assuming z achieves a steady concentration over time, z settles down to satisfy

(which is deduced by setting the derivative of z with respect to time to zero).

So the important question is under what parameter values does the original population persist (continue to exist)? The population persists if and only if the steady state value of z is strictly positive. i.e. if and only if:

This result is more popularly expressed in terms of the ratio of a:b and the error rate q of individual digits: set b/a = (1-s), then the condition becomes

Taking a logarithm on both sides and approximating for small q and s one gets

reducing the condition to:

RNA viruses which replicate close to the error threshold have a genome size of order 104 base pairs. Human DNA is about 3.3 billion (109) base units long. This means that the replication mechanism for DNA must be orders of magnitude more accurate than for RNA.

Read more about this topic: Error Catastrophe

Famous quotes containing the words basic, mathematical and/or model:

“The basic Female body comes with the following accessories: garter belt, panti-girdle, crinoline, camisole, bustle, brassiere, stomacher, chemise, virgin zone, spike heels, nose ring, veil, kid gloves, fishnet stockings, fichu, bandeau, Merry Widow, weepers, chokers, barrettes, bangles, beads, lorgnette, feather boa, basic black, compact, Lycra stretch one-piece with modesty panel, designer peignoir, flannel nightie, lace teddy, bed, head.”
—Margaret Atwood (b. 1939)

“What is history? Its beginning is that of the centuries of systematic work devoted to the solution of the enigma of death, so that death itself may eventually be overcome. That is why people write symphonies, and why they discover mathematical infinity and electromagnetic waves.”
—Boris Pasternak (1890–1960)

“When Titian was mixing brown madder,
His model was posed up a ladder.
Said Titian, “That position
Calls for coition,”
So he lept up the ladder and had her.”
—Anonymous.