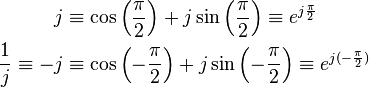Electrical Impedance - Device Examples

Device Examples

The impedance of an ideal resistor is purely real and is referred to as a resistive impedance:

In this case, the voltage and current waveforms are proportional and in phase.

Ideal inductors and capacitors have a purely imaginary reactive impedance:

the impedance of inductors increases as frequency increases;

the impedance of capacitors decreases as frequency increases;

In both cases, for an applied sinusoidal voltage, the resulting current is also sinusoidal, but in quadrature, 90 degrees out of phase with the voltage. However, the phases have opposite signs: in an inductor, the current is lagging; in a capacitor the current is leading.

Note the following identities for the imaginary unit and its reciprocal:

\begin{align} j &\equiv \cos{\left( \frac{\pi}{2}\right)} + j\sin{\left( \frac{\pi}{2}\right)} \equiv e^{j \frac{\pi}{2}} \\ \frac{1}{j} \equiv -j &\equiv \cos{\left(-\frac{\pi}{2}\right)} + j\sin{\left(-\frac{\pi}{2}\right)} \equiv e^{j(-\frac{\pi}{2})} \end{align}

Thus the inductor and capacitor impedance equations can be rewritten in polar form:

\begin{align} Z_L &= \omega Le^{j\frac{\pi}{2}} \\ Z_C &= \frac{1}{\omega C}e^{j\left(-\frac{\pi}{2}\right)} \end{align}

The magnitude gives the change in voltage amplitude for a given current amplitude through the impedance, while the exponential factors give the phase relationship.

Read more about this topic:  Electrical Impedance

Famous quotes containing the words device and/or examples:

    “The man who pretends that the distribution of income in this country reflects the distribution of ability or character is an ignoramus. The man who says that it could by any possible political device be made to do so is an unpractical visionary. But the man who says that it ought to do so is something worse than an ignoramous and more disastrous than a visionary: he is, in the profoundest Scriptural sense of the word, a fool.”
    —George Bernard Shaw (1856–1950)

    “There are many examples of women that have excelled in learning, and even in war, but this is no reason we should bring ‘em all up to Latin and Greek or else military discipline, instead of needle-work and housewifry.”
    —Bernard Mandeville (1670–1733)