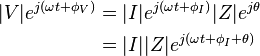Complex Voltage and Current
In order to simplify calculations, sinusoidal voltage and current waves are commonly represented as complex-valued functions of time denoted as and .
Impedance is defined as the ratio of these quantities.
Substituting these into Ohm's law we have
Noting that this must hold for all, we may equate the magnitudes and phases to obtain
The magnitude equation is the familiar Ohm's law applied to the voltage and current amplitudes, while the second equation defines the phase relationship.
Read more about this topic: Electrical Impedance
Famous quotes containing the words complex and/or current:
“Uneducated people are unfortunate in that they do grasp complex issues, educated people, on the other hand, often do not understand simplicity, which is a far greater misfortune.”
—Franz Grillparzer (1791–1872)
“It is not however, adulthood itself, but parenthood that forms the glass shroud of memory. For there is an interesting quirk in the memory of women. At 30, women see their adolescence quite clearly. At 30 a woman’s adolescence remains a facet fitting into her current self.... At 40, however, memories of adolescence are blurred. Women of this age look much more to their earlier childhood for memories of themselves and of their mothers. This links up to her typical parenting phase.”
—Terri Apter (20th century)