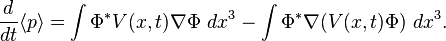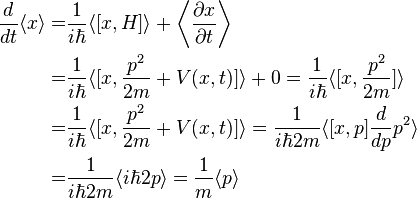Ehrenfest Theorem - General Example

General Example

For the very general example of a massive particle moving in a potential, the Hamiltonian is simply

where is just the location of the particle. Suppose we wanted to know the instantaneous change in momentum . Using Ehrenfest's theorem, we have

since the operator commutes with itself and has no time dependence. By expanding the right-hand-side, replacing p by, we get

$\frac{d}{dt}\langle p\rangle = \int \Phi^* V(x,t)\nabla\Phi~dx^3 - \int \Phi^* \nabla (V(x,t)\Phi)~dx^3.$

After applying the product rule on the second term, we have

$\begin{align} \frac{d}{dt}\langle p\rangle =& \int \Phi^* V(x,t)\nabla\Phi~dx^3 - \int \Phi^* (\nabla V(x,t))\Phi ~dx^3 - \int \Phi^* V(x,t)\nabla\Phi~dx^3 \\ =& - \int \Phi^* (\nabla V(x,t))\Phi ~dx^3 \\ =& \langle -\nabla V(x,t)\rangle = \langle F \rangle, \end{align}$

but we recognize this as Newton's second law. This is an example of the correspondence principle, the result manifests as Newton's second law in the case of having so many particles that the net motion is given exactly by the expectation value of a single particle.

Similarly we can obtain the instantaneous change in the position expectation value.

$\begin{align} \frac{d}{dt}\langle x\rangle =& \frac{1}{i\hbar}\langle \rangle + \left\langle \frac{\partial x}{\partial t}\right\rangle \\ =& \frac{1}{i\hbar}\langle \rangle + 0 = \frac{1}{i\hbar}\langle \rangle \\ =& \frac{1}{i\hbar}\langle \rangle = \frac{1}{i\hbar 2 m}\langle \frac{d}{dp} p^2\rangle \\ =& \frac{1}{i\hbar 2 m}\langle i \hbar 2 p\rangle = \frac{1}{m}\langle p\rangle \end{align}$

This result is again in accord with the classical equation.

Read more about this topic: Ehrenfest Theorem

Famous quotes containing the word general:

“No government can help the destinies of people who insist in putting sectional and class consciousness ahead of general weal.”
—Franklin D. Roosevelt (1882–1945)

“One general builds his success on ten thousand bleaching bones.”
—Chinese proverb.