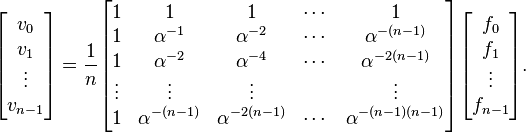Discrete Fourier Transform (general) - Matrix Formulation

Matrix Formulation

Since the discrete Fourier transform is a linear operator, it can be described by matrix multiplication. In matrix notation, the discrete Fourier transform is expressed as follows:

\begin{bmatrix}f_0\\f_1\\\vdots\\f_{n-1}\end{bmatrix} = \begin{bmatrix} 1&1&1&\cdots &1 \\ 1&\alpha&\alpha^2&\cdots&\alpha^{n-1} \\ 1&\alpha^2&\alpha^4&\cdots&\alpha^{2(n-1)}\\ \vdots&\vdots&\vdots&&\vdots\\ 1&\alpha^{n-1}&\alpha^{2(n-1)}&\cdots&\alpha^{(n-1)(n-1)}\\ \end{bmatrix} \begin{bmatrix}v_0\\v_1\\\vdots\\v_{n-1}\end{bmatrix}.

The matrix for this transformation is called the DFT matrix.

Similarly, the matrix notation for the inverse Fourier transform is

\begin{bmatrix}v_0\\v_1\\\vdots\\v_{n-1}\end{bmatrix} = \frac{1}{n}\begin{bmatrix} 1&1&1&\cdots &1 \\ 1&\alpha^{-1}&\alpha^{-2}&\cdots&\alpha^{-(n-1)} \\ 1&\alpha^{-2}&\alpha^{-4}&\cdots&\alpha^{-2(n-1)}\\ \vdots&\vdots&\vdots&&\vdots\\ 1&\alpha^{-(n-1)}&\alpha^{-2(n-1)}&\cdots&\alpha^{-(n-1)(n-1)} \end{bmatrix} \begin{bmatrix}f_0\\f_1\\\vdots\\f_{n-1}\end{bmatrix}.

Read more about this topic:  Discrete Fourier Transform (general)

Famous quotes containing the words matrix and/or formulation:

    “In all cultures, the family imprints its members with selfhood. Human experience of identity has two elements; a sense of belonging and a sense of being separate. The laboratory in which these ingredients are mixed and dispensed is the family, the matrix of identity.”
    —Salvador Minuchin (20th century)

    “You do not mean by mystery what a Catholic does. You mean an interesting uncertainty: the uncertainty ceasing interest ceases also.... But a Catholic by mystery means an incomprehensible certainty: without certainty, without formulation there is no interest;... the clearer the formulation the greater the interest.”
    —Gerard Manley Hopkins (1844–1889)