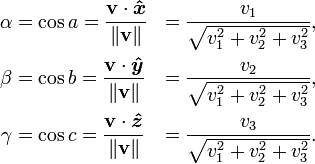Direction Cosine

In analytic geometry, the direction cosines (or directional cosines) of a vector are the cosines of the angles between the vector and the three coordinate axes. Or equivalently it is the component contributions of the basis to the unit vector.

If v is a vector

where are basis, then the direction cosines are

\begin{align} \alpha & = \cos a = \frac{{\mathbf v} \cdot \boldsymbol{\hat{x}} }{ \left \Vert {\mathbf v} \right \Vert } & = \frac{v_1}{\sqrt{v_1^2 + v_2^2 + v_3^2}} ,\\ \beta & = \cos b = \frac{{\mathbf v} \cdot \boldsymbol{\hat{y}} }{ \left \Vert {\mathbf v} \right \Vert } & = \frac{v_2}{\sqrt{v_1^2 + v_2^2 + v_3^2}} ,\\ \gamma &= \cos c = \frac{{\mathbf v} \cdot \boldsymbol{\hat{z}} }{ \left \Vert {\mathbf v} \right \Vert } & = \frac{v_3}{\sqrt{v_1^2 + v_2^2 + v_3^2}}. \end{align}

Note that

\cos ^2 a + \cos ^2 b + \cos ^2 c = 1

and

(, ) is the Cartesian coordinates of the unit vector .

More generally, direction cosine refers to the cosine of the angle between any two vectors. They are useful for forming direction cosine matrices that express one set of orthonormal basis vectors in terms of another set, or for expressing a known vector in a different basis.

Famous quotes containing the word direction:

    “German poetry is going in a very different direction from French poetry.... Its language has become more sober, more factual. It distrusts “beauty.” It tries to be truthful.”
    —Paul Celan [Paul Antschel] (1920–1970)