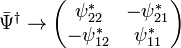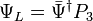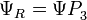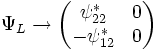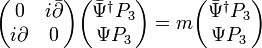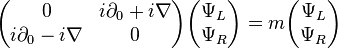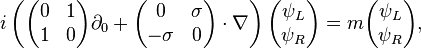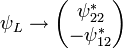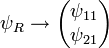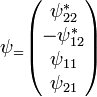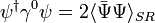Dirac Equation in The Algebra of Physical Space - Relation With The Standard Form

Relation With The Standard Form

The spinor can be written in a null basis as

\Psi = \psi_{11} P_3 - \psi_{12} P_3 \mathbf{e}_1 + \psi_{21} \mathbf{e}_1 P_3 + \psi_{22} \bar{P}_3,

such that the representation of the spinor in terms of the Pauli matrices is

\Psi \rightarrow \begin{pmatrix} \psi_{11} & \psi_{12} \\ \psi_{21} & \psi_{22} \end{pmatrix}
\bar{\Psi}^\dagger \rightarrow \begin{pmatrix} \psi_{22}^* & -\psi_{21}^* \\ -\psi_{12}^* & \psi_{11}^* \end{pmatrix}

The standard form of the Dirac equation can be recovered by decomposing the spinor in its right and left-handed spinor components, which are extracted with the help of the projector

such that

\Psi_L = \bar{\Psi}^\dagger P_3
\Psi_R = \Psi P_3^{ }

with the following matrix representation

\Psi_L \rightarrow \begin{pmatrix} \psi_{22}^* & 0 \\ -\psi_{12}^* & 0 \end{pmatrix}
\Psi_R \rightarrow \begin{pmatrix} \psi_{11} & 0 \\ \psi_{21} & 0 \end{pmatrix}

The Dirac equation can be also written as

Without electromagnetic interaction, the following equation is obtained from the two equivalent forms of the Dirac equation

\begin{pmatrix} 0 & i \bar{\partial}\\ i \partial & 0 \end{pmatrix} \begin{pmatrix} \bar{\Psi}^\dagger P_3 \\ \Psi P_3 \end{pmatrix} = m \begin{pmatrix} \bar{\Psi}^\dagger P_3 \\ \Psi P_3 \end{pmatrix}

so that

\begin{pmatrix} 0 & i \partial_0 + i\nabla \\ i \partial_0 - i \nabla & 0 \end{pmatrix} \begin{pmatrix} \Psi_L \\ \Psi_R \end{pmatrix} = m \begin{pmatrix} \Psi_L \\ \Psi_R \end{pmatrix}

or in matrix representation

i \left( \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \partial_0 + \begin{pmatrix} 0 & \sigma \\ -\sigma & 0 \end{pmatrix} \cdot \nabla \right) \begin{pmatrix} \psi_L \\ \psi_R \end{pmatrix} = m \begin{pmatrix} \psi_L \\ \psi_R \end{pmatrix},

where the second column of the right and left spinors can be dropped by defining the single column chiral spinors as

\psi_L \rightarrow \begin{pmatrix} \psi_{22}^* \\ -\psi_{12}^* \end{pmatrix}
\psi_R \rightarrow \begin{pmatrix} \psi_{11} \\ \psi_{21} \end{pmatrix}

The standard relativistic covariant form of the Dirac equation in the Weyl representation can be easily identified i \gamma^{\mu} \partial_{\mu} \psi = m \psi, such that

\psi_= \begin{pmatrix} \psi_{22}^* \\ -\psi_{12}^* \\ \psi_{11} \\ \psi_{21} \end{pmatrix}

Given two spinors and in APS and their respective spinors in the standard form as and, one can verify the following identity

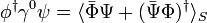\phi^\dagger \gamma^0 \psi = \langle \bar{\Phi}\Psi + (\bar{\Psi}\Phi)^\dagger \rangle_S ,

such that

\psi^\dagger \gamma^0 \psi = 2 \langle \bar{\Psi}\Psi \rangle_{S R}

Read more about this topic:  Dirac Equation In The Algebra Of Physical Space

Famous quotes containing the words relation with the, relation with, relation, standard and/or form:

    “There is a constant in the average American imagination and taste, for which the past must be preserved and celebrated in full-scale authentic copy; a philosophy of immortality as duplication. It dominates the relation with the self, with the past, not infrequently with the present, always with History and, even, with the European tradition.”
    —Umberto Eco (b. 1932)

    “There is a constant in the average American imagination and taste, for which the past must be preserved and celebrated in full-scale authentic copy; a philosophy of immortality as duplication. It dominates the relation with the self, with the past, not infrequently with the present, always with History and, even, with the European tradition.”
    —Umberto Eco (b. 1932)

    “Any relation to the land, the habit of tilling it, or mining it, or even hunting on it, generates the feeling of patriotism. He who keeps shop on it, or he who merely uses it as a support to his desk and ledger, or to his manufactory, values it less.”
    —Ralph Waldo Emerson (1803–1882)

    “Gentlemen, those confederate flags and our national standard are what has made this union great. In what other country could a man who fought against you be permitted to serve as judge over you, be permitted to run for reelection and bespeak your suffrage on Tuesday next at the poles.”
    —Laurence Stallings (1894–1968)

    “In every form of womanly love something of motherly love also comes to light.”
    —Friedrich Nietzsche (1844–1900)