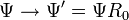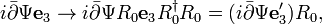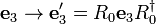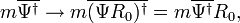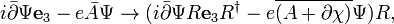Dirac Equation in The Algebra of Physical Space

Electromagnetic Gauge

The Dirac equation is invariant under a global right rotation applied on the spinor of the type

$\Psi \rightarrow \Psi^\prime = \Psi R_0$

so that the kinetic term of the Dirac equation transforms as

$i\bar{\partial} \Psi \mathbf{e}_3 \rightarrow i\bar{\partial} \Psi R_0 \mathbf{e}_3 R_0^\dagger R_0 = ( i\bar{\partial} \Psi \mathbf{e}_3^\prime ) R_0,$

where we identify the following rotation

$\mathbf{e}_3 \rightarrow \mathbf{e}_3^\prime = R_0 \mathbf{e}_3 R_0^\dagger$

The mass term transforms as

$m \overline{\Psi^\dagger} \rightarrow m \overline{(\Psi R_0)^\dagger} = m \overline{ \Psi^\dagger }R_0,$

so that we can verify the invariance of the form of the Dirac equation. A more demanding requirement is that the Dirac equation should be invariant under a local gauge transformation of the type

In this case, the kinetic term transforms as

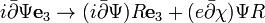$i\bar{\partial} \Psi \mathbf{e}_3 \rightarrow (i \bar{\partial} \Psi) R \mathbf{e}_3 + (e\bar{\partial}\chi) \Psi R$ ,

so that the left side of the Dirac equation transforms covariantly as

$i\bar{\partial} \Psi \mathbf{e}_3 -e \bar{A}\Psi \rightarrow (i\bar{\partial} \Psi R \mathbf{e}_3 R^\dagger -e \overline{(A + \partial \chi)}\Psi)R,$

where we identify the need to perform an electromagnetic gauge transformation. The mass term transforms as in the case with global rotation, so, the form of the Dirac equation remains invariant.

Read more about this topic: Dirac Equation In The Algebra Of Physical Space

Dirac Equation in The Algebra of Physical Space - Electromagnetic Gauge