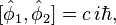Dirac Bracket - The Dirac Bracket

The Dirac Bracket

Above is everything needed to find the equations of motion in Dirac's modified Hamiltonian procedure. Having the equations of motion, however, is not the endpoint for theoretical considerations. If one wants to canonically quantize a general system, then one needs the Dirac brackets.

Before defining Dirac brackets, first-class and second-class constraints need to be introduced. We call a function f(q, p) of coordinates and momenta first class if its Poisson bracket with all of the constraints weakly vanishes, that is,

for all . Note that the only quantities that weakly vanish are the constraints, and therefore anything that weakly vanishes must be strongly equal to a linear combination of the constraints. One can demonstrate that the Poisson bracket of two first class quantities must also be first class. The first class constraints are intimately connected with the unphysical degrees of freedom mentioned earlier. Namely, the number of independent first class constraints is equal to the number of unphysical degrees of freedom, and furthermore the primary first class constraints generate gauge transformations. Dirac further postulated that all secondary first class constraints are generators of gauge transformations, which turns out to be false; however, typically one operates under the assumption that all first class constraints generate gauge transformations when using this treatment.

When the first-class secondary constraints are added into the Hamiltonian with arbitrary as the first class primary constraints are added to arrive at the total Hamiltonian, then one obtains the extended Hamiltonian. The extended Hamiltonian gives the most general possible time evolution for any gauge-dependent quantities, and may actually generalize the equations of motion from those of the Lagrangian formalism.

For the purposes of introducing the Dirac bracket, of more immediate interest are the second class constraints. Second class constraints are constraints that have nonvanishing Poisson bracket with at least one other constraint. For instance, consider constraints and whose Poisson bracket is simply a constant, c,

Now, suppose one wishes to employ canonical quantization, then the phase space coordinates become operators whose commutators become iħ times their classical Poisson bracket. Assuming there are no ordering issues that give rise to new quantum corrections, this implies that

where the hats emphasize the fact that the constraints are operators. On the one hand, canonical quantization gives the above commutation relation, but on the other hand and are constraints that must vanish on physical states, whereas the right hand side cannot vanish. This example illustrates the need for a generalization of the Poisson bracket that respects the system's constraints, and leads to a consistent quantization procedure.

The new bracket should be bilinear, antisymmetric, satisfy the Jacobi identity as does the Poisson bracket, reduce to the Poisson bracket for unconstrained systems, and additionally the bracket of any constraint with any other quantity must vanish.

At this point, the second class constraints will be labeled . Define a matrix with entries

In this case, the Dirac bracket of two functions on phase space, f and g, is defined as

where denotes the ab entry of M 's inverse matrix. Dirac proved that M will always be invertible.

It is straightforward to check that the above definition of the Dirac bracket satisfies all of the desired properties, and especially the last one, of vanishing for an argument which is a constraint. When using canonical quantization with a constrained Hamiltonian system, the commutator of the operators is supplanted by iħ times their classical Dirac bracket. Since the Dirac bracket respects the constraints, one need not be careful about evaluating all brackets before using any weak equations, as is the case with the Poisson bracket.

Note that while the Poisson bracket of bosonic (Grassmann even) variables with itself must vanish, the Poisson bracket of fermions represented as a Grassmann variables with itself need not vanish. This means that in the fermionic case it is possible for there to be an odd number of second class constraints.