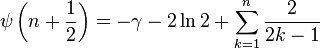Digamma Function - Relation To Harmonic Numbers

Relation To Harmonic Numbers

The digamma function, often denoted also as ψ0(x), ψ0(x) or (after the shape of the archaic Greek letter Ϝ digamma), is related to the harmonic numbers in that

where Hn is the n harmonic number, and γ is the Euler-Mascheroni constant. For half-integer values, it may be expressed as

\psi\left(n+{\frac{1}{2}}\right) = -\gamma - 2\ln 2 + \sum_{k=1}^n \frac{2}{2k-1}

Read more about this topic:  Digamma Function

Famous quotes containing the words relation to, relation, harmonic and/or numbers:

    “Much poetry seems to be aware of its situation in time and of its relation to the metronome, the clock, and the calendar. ... The season or month is there to be felt; the day is there to be seized. Poems beginning “When” are much more numerous than those beginning “Where” of “If.” As the meter is running, the recurrent message tapped out by the passing of measured time is mortality.”
    —William Harmon (b. 1938)

    “There is undoubtedly something religious about it: everyone believes that they are special, that they are chosen, that they have a special relation with fate. Here is the test: you turn over card after card to see in which way that is true. If you can defy the odds, you may be saved. And when you are cleaned out, the last penny gone, you are enlightened at last, free perhaps, exhilarated like an ascetic by the falling away of the material world.”
    —Andrei Codrescu (b. 1947)

    “For decades child development experts have erroneously directed parents to sing with one voice, a unison chorus of values, politics, disciplinary and loving styles. But duets have greater harmonic possibilities and are more interesting to listen to, so long as cacophony or dissonance remains at acceptable levels.”
    —Kyle D. Pruett (20th century)

    “All experience teaches that, whenever there is a great national establishment, employing large numbers of officials, the public must be reconciled to support many incompetent men; for such is the favoritism and nepotism always prevailing in the purlieus of these establishments, that some incompetent persons are always admitted, to the exclusion of many of the worthy.”
    —Herman Melville (1819–1891)