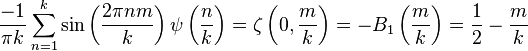Digamma Function - Gaussian Sum

Gaussian Sum

The digamma has a Gaussian sum of the form

$\frac{-1}{\pi k} \sum_{n=1}^k \sin \left( \frac{2\pi nm}{k}\right) \psi \left(\frac{n}{k}\right) = \zeta\left(0,\frac{m}{k}\right) = -B_1 \left(\frac{m}{k}\right) = \frac{1}{2} - \frac{m}{k}$

for integers . Here, ζ(s,q) is the Hurwitz zeta function and is a Bernoulli polynomial. A special case of the multiplication theorem is

$\sum_{n=1}^k \psi \left(\frac{n}{k}\right) =-k(\gamma+\log k),$

and a neat generalization of this is

where q must be a natural number, but 1-qa not.

Read more about this topic: Digamma Function

Famous quotes containing the word sum:

“We didn’t come to dig in Egypt for medals. Much more is learned from studying bits of broken pottery than from all the sensational finds. Our job is to increase the sum of human knowledge of the past, not to satisfy our own curiosity.”
—John L. Balderston (1899–1954)