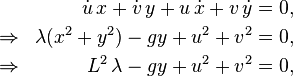Differential Algebraic Equation - Examples

Examples

The pendulum in Cartesian coordinates (x,y) with center in (0,0) and length L has the Euler-Lagrange equations

\begin{align} \dot x&=u,&\dot y&=v,\\ \dot u&=\lambda x,&\dot v&=\lambda y-g,\\ x^2+y^2&=L^2, \end{align}

where is a Lagrange multiplier. The momentum variables u and v should be constrained by the law of conservation of energy and their direction should point along the circle. Neither condition is explicit in those equations. Differentiation of the last equation leads to

\begin{align} &&\dot x\,x+\dot y\,y&=0\\ \Rightarrow&& u\,x+v\,y&=0, \end{align}

restricting the direction of motion to the tangent of the circle. The next derivative of this equation implies

\begin{align} &&\dot u\,x+\dot v\,y+u\,\dot x+v\,\dot y&=0,\\ \Rightarrow&& \lambda(x^2+y^2)-gy+u^2+v^2&=0,\\ \Rightarrow&& L^2\,\lambda-gy+u^2+v^2&=0, \end{align}

and the derivative of that last identity simplifies to which implicitly implies the conservation of energy since after integration the constant is the sum of kinetic and potential energy.

To obtain unique derivative values for all dependent variables the last equation was three times differentiated. This gives a differentiation index of 3, which is typical for constrained mechanical systems.

If initial values and a sign for y are given, the other variables are determined via, and if then and . To proceed to the next point it is sufficient to get the derivatives of x and u, that is, the system to solve is now

\begin{align} \dot x&=u,\\ \dot u&=\lambda x,\\ 0&=x^2+y^2-L^2,\\ 0&=ux+vy,\\ 0&=u^2-gy+v^2+L^2\,\lambda. \end{align}

This is a semi-explicit DAE of index 1. Another set of similar equations may be obtained starting from and a sign for x.

Read more about this topic:  Differential Algebraic Equation

Famous quotes containing the word examples:

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)

    “It is hardly to be believed how spiritual reflections when mixed with a little physics can hold people’s attention and give them a livelier idea of God than do the often ill-applied examples of his wrath.”
    —G.C. (Georg Christoph)