Dice Cup - Probability

Probability

For a single roll of a fair s-sided die, the probability of rolling each value is exactly 1/s; this is an example of a discrete uniform distribution. For n multiple rolls, with a s-sided die the possibility space is equal to sn. So, for n rolls of an s-sided die the probability of any result is 1/sn.

However, if we are rolling two dice and adding the result together, as in the game craps, the total is distributed in a triangular curve; the case for common dice follows:

Sum 2 3 4 5 6 7 8 9 10 11 12
Probability 1/36
 2/36
=1/18		 3/36
=1/12		 4/36
=1/9		 5/36
 6/36
=1/6		 5/36
 4/36
=1/9		 3/36
=1/12		 2/36
=1/18		 1/36

As the number of dice increases, the distribution of the sum of all numbers tends to normal distribution by the central limit theorem; the exact value of a sum of n s-sided dice, k, is

where Fs,1(k) = 1/s for 1 ≤ k ≤ s and 0 otherwise.

A faster algorithm would adapt the exponentiation by squaring algorithm:

.

In the triangular curve described above,

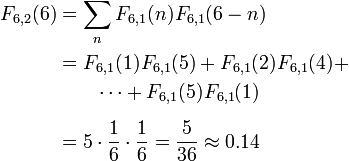
\begin{align} F_{6,2}(6) & =\sum_n {F_{6,1}(n) F_{6,1}(6 - n)} \\ & =F_{6,1}(1) F_{6,1}(5) + F_{6,1}(2) F_{6,1}(4) + \\ & \qquad \cdots + F_{6,1}(5) F_{6,1}(1) \\ & = 5\cdot\frac{1}{6}\cdot\frac{1}{6}=\frac{5}{36}\approx0.14 \end{align}

Equivalently, the probability can be calculated using combinations:

where is the floor function. The probability of rolling an exact sequence of numbers is 1/sn.

Read more about this topic:  Dice Cup

Famous quotes containing the word probability:

    “Liberty is a blessing so inestimable, that, wherever there appears any probability of recovering it, a nation may willingly run many hazards, and ought not even to repine at the greatest effusion of blood or dissipation of treasure.”
    —David Hume (1711–1776)

    “Only in Britain could it be thought a defect to be “too clever by half.” The probability is that too many people are too stupid by three-quarters.”
    —John Major (b. 1943)

    “The probability of learning something unusual from a newspaper is far greater than that of experiencing it; in other words, it is in the realm of the abstract that the more important things happen in these times, and it is the unimportant that happens in real life.”
    —Robert Musil (1880–1942)