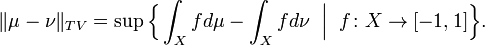Convergence of Measures - Total Variation Convergence of Measures

Total Variation Convergence of Measures

This is the strongest notion of convergence shown on this page and is defined as follows. Let be a measurable space. The total variation distance between two (positive) measures and is then given by

Here the supremum is taken over ranging over the set of all measurable functions from to . This is in contrast, for example, to the Wasserstein metric, where the definition is of the same form, but the supremum is taken over ranging over the set of measurable functions from to which have Lipschitz constant at most 1; and also in contrast to the Radon metric, where the supremum is taken over ranging over the set of continuous functions from to . In the case where is a Polish space, the total variation metric coincides with the Radon metric.

If and are both probability measures, then the total variation distance is also given by

The equivalence between these two definitions can be seen as a particular case of the Monge-Kantorovich duality. From the two definitions above, it is clear that the total variation distance between probability measures is always between 0 and 2.

To illustrate the meaning of the total variation distance, consider the following thought experiment. Assume that we are given two probability measures and, as well as a random variable . We know that has law either or, but we do not know which one of the two. Assume now that we are given one single sample distributed according to the law of and that we are then asked to guess which one of the two distributions describes that law. The quantity

then provides a sharp upper bound on the probability that our guess is correct.

Given the above definition of total variation distance, a sequence of measures defined on the same measure space is said to converge to a measure in total variation distance if for every, there exists an such that for all, one has that .