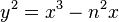Relation To Elliptic Curves
The question of whether a given number is congruent turns out to be equivalent to the condition that a certain elliptic curve has positive rank. An alternative approach to the idea is presented below (as can essentially also be found in the introduction to Tunnell's paper).
Suppose a,b,c are numbers (not necessarily positive or rational) which satisfy the following two equations:
Then set x = n(a+c)/b and y = 2n2(a+c)/b2. A calculation shows
and y is not 0 (if y = 0 then a = -c, so b = 0, but (1/2)ab = n is nonzero, a contradiction).
Conversely, if x and y are numbers which satisfy the above equation and y is not 0, set a = (x2 - n2)/y, b = 2nx/y, and c = (x2 + n2)/y . A calculation shows these three numbers satisfy the two equations for a, b, and c above.
These two correspondences between (a,b,c) and (x,y) are inverses of each other, so we have a one-to-one correspondence between any solution of the two equations in a, b, and c and any solution of the equation in x and y with y nonzero. In particular, from the formulas in the two correspondences, for rational n we see that a, b, and c are rational if and only if the corresponding x and y are rational, and vice versa. (We also have that a, b, and c are all positive if and only if x and y are all positive; notice from the equation y2 = x3 - xn2 = x(x2 - n2) that if x and y are positive then x2 - n2 must be positive, so the formula for a above is positive.)
Thus a positive rational number n is congruent if and only if the equation y2 = x3 - n2x has a rational point with y not equal to 0. It can be shown (as a nice application of Dirichlet's theorem on primes in arithmetic progression) that the only torsion points on this elliptic curve are those with y equal to 0, hence the existence of a rational point with y nonzero is equivalent to saying the elliptic curve has positive rank.
Read more about this topic: Congruent Number
Famous quotes containing the words relation to, relation and/or curves:
“Only in a house where one has learnt to be lonely does one have this solicitude for things. One’s relation to them, the daily seeing or touching, begins to become love, and to lay one open to pain.”
—Elizabeth Bowen (1899–1973)
“Skepticism is unbelief in cause and effect. A man does not see, that, as he eats, so he thinks: as he deals, so he is, and so he appears; he does not see that his son is the son of his thoughts and of his actions; that fortunes are not exceptions but fruits; that relation and connection are not somewhere and sometimes, but everywhere and always; no miscellany, no exemption, no anomaly,—but method, and an even web; and what comes out, that was put in.”
—Ralph Waldo Emerson (1803–1882)
“For a hundred and fifty years, in the pasture of dead horses,
roots of pine trees pushed through the pale curves of your ribs,
yellow blossoms flourished above you in autumn, and in winter
frost heaved your bones in the ground—old toilers, soil makers:
O Roger, Mackerel, Riley, Ned, Nellie, Chester, Lady Ghost.”
—Donald Hall (b. 1928)