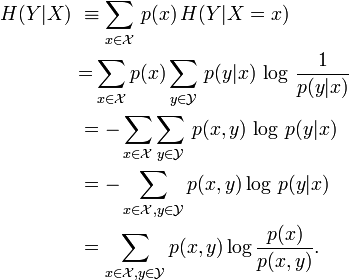Conditional Entropy - Definition

Definition

If is the entropy of the variable conditioned on the variable taking a certain value, then is the result of averaging over all possible values that may take.

Given discrete random variable with support and with support, the conditional entropy of given is defined as:

\begin{align} H(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,H(Y|X=x)\\ &{=}\sum_{x\in\mathcal X}p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, \frac{1}{p(y|x)}\\ &=-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\ &=-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\ &=\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\ \end{align}


Note: The supports of X and Y can be replaced by their domains if it is understood that should be treated as being equal to zero.

if and only if the value of is completely determined by the value of . Conversely, if and only if and are independent random variables.

Read more about this topic:  Conditional Entropy

Famous quotes containing the word definition:

    “Mothers often are too easily intimidated by their children’s negative reactions...When the child cries or is unhappy, the mother reads this as meaning that she is a failure. This is why it is so important for a mother to know...that the process of growing up involves by definition things that her child is not going to like. Her job is not to create a bed of roses, but to help him learn how to pick his way through the thorns.”
    —Elaine Heffner (20th century)

    “One definition of man is “an intelligence served by organs.””
    —Ralph Waldo Emerson (1803–1882)

    “It is very hard to give a just definition of love. The most we can say of it is this: that in the soul, it is a desire to rule; in the spirit, it is a sympathy; and in the body, it is but a hidden and subtle desire to possess—after many mysteries—what one loves.”
    —François, Duc De La Rochefoucauld (1613–1680)