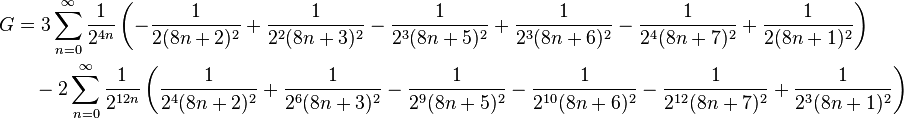Catalan's Constant - Quickly Converging Series

Quickly Converging Series

The following two formulas involve quickly converging series, and are thus appropriate for numerical computation:

\begin{align} G & = 3 \sum_{n=0}^\infty \frac{1}{2^{4n}} \left( -\frac{1}{2(8n+2)^2} +\frac{1}{2^2(8n+3)^2} -\frac{1}{2^3(8n+5)^2} +\frac{1}{2^3(8n+6)^2} -\frac{1}{2^4(8n+7)^2} +\frac{1}{2(8n+1)^2} \right) \\ & {}\quad -2 \sum_{n=0}^\infty \frac{1}{2^{12n}} \left( \frac{1}{2^4(8n+2)^2} +\frac{1}{2^6(8n+3)^2} -\frac{1}{2^9(8n+5)^2} -\frac{1}{2^{10} (8n+6)^2} -\frac{1}{2^{12} (8n+7)^2} +\frac{1}{2^3(8n+1)^2} \right) \end{align}

and

The theoretical foundations for such series is given by Broadhurst (the first formula) and Ramanujan (the second formula). The algorithms for fast evaluation of the Catalan constant is constructed by E. Karatsuba.

Read more about this topic:  Catalan's Constant

Famous quotes containing the words quickly, converging and/or series:

    “Give up the belief that mind is, even temporarily, compressed within the skull, and you will quickly become more manly or womanly. You will understand yourself and your Maker better than before.”
    —Mary Baker Eddy (1821–1910)

    “It might become a wheel spoked red and white
    In alternate stripes converging at a point
    Of flame on the line, with a second wheel below,
    Just rising, accompanying, arranged to cross,
    Through weltering illuminations, humps
    Of billows, downward, toward the drift-fire shore.”
    —Wallace Stevens (1879–1955)

    “The theory of truth is a series of truisms.”
    —J.L. (John Langshaw)