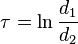Bipolar Coordinates - Definition

Definition

The most common definition of bipolar coordinates (σ, τ) is

x = a \ \frac{\sinh \tau}{\cosh \tau - \cos \sigma}
y = a \ \frac{\sin \sigma}{\cosh \tau - \cos \sigma}

where the σ-coordinate of a point P equals the angle F1 P F2 and the τ-coordinate equals the natural logarithm of the ratio of the distances d1 and d2 to the foci

\tau = \ln \frac{d_1}{d_2}

(Recall that F1 and F2 are located at (−a, 0) and (a, 0), respectively.) Equivalently

x + i y = a i \cot\left( \frac{\sigma + i \tau}{2}\right)

Read more about this topic:  Bipolar Coordinates

Famous quotes containing the word definition:

    “Beauty, like all other qualities presented to human experience, is relative; and the definition of it becomes unmeaning and useless in proportion to its abstractness. To define beauty not in the most abstract, but in the most concrete terms possible, not to find a universal formula for it, but the formula which expresses most adequately this or that special manifestation of it, is the aim of the true student of aesthetics.”
    —Walter Pater (1839–1894)

    “The very definition of the real becomes: that of which it is possible to give an equivalent reproduction.... The real is not only what can be reproduced, but that which is always already reproduced. The hyperreal.”
    —Jean Baudrillard (b. 1929)

    “Although there is no universal agreement as to a definition of life, its biological manifestations are generally considered to be organization, metabolism, growth, irritability, adaptation, and reproduction.”
    —The Columbia Encyclopedia, Fifth Edition, the first sentence of the article on “life” (based on wording in the First Edition, 1935)