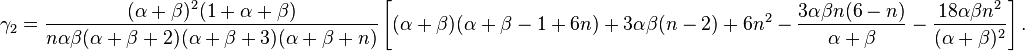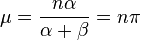Beta-binomial Distribution - Moments and Properties

Moments and Properties

The first three raw moments are

$\begin{align} \mu_1 & =\frac{n\alpha}{\alpha+\beta} \\ \mu_2 & =\frac{n\alpha}{(\alpha+\beta)(1+\alpha+\beta)}\\ \mu_3 & =\frac{n\alpha}{(\alpha+\beta)(1+\alpha+\beta)(2+\alpha+\beta)} \end{align}$

and the kurtosis is

$\gamma_2 = \frac{(\alpha + \beta)^2 (1+\alpha+\beta)}{n \alpha \beta( \alpha + \beta + 2)(\alpha + \beta + 3)(\alpha + \beta + n) } \left.$

Letting we note, suggestively, that the mean can be written as

$\mu = \frac{n\alpha}{\alpha+\beta}=n\pi \!$

and the variance as

$\sigma^2 = \frac{n\alpha\beta(\alpha+\beta+n)}{(\alpha+\beta)^2(\alpha+\beta+1)} = n\pi(1-\pi) \frac{\alpha + \beta + n}{\alpha + \beta + 1} = n\pi(1-\pi) \!$

where is the pairwise correlation between the n Bernoulli draws and is called the over-dispersion parameter.

Read more about this topic: Beta-binomial Distribution

Famous quotes containing the words moments and/or properties:

“Reminiscences, even extensive ones, do not always amount to an autobiography.... For autobiography has to do with time, with sequence and what makes up the continuous flow of life. Here, I am talking of a space, of moments and discontinuities. For even if months and years appear here, it is in the form they have in the moment of recollection. This strange form—it may be called fleeting or eternal—is in neither case the stuff that life is made of.”
—Walter Benjamin (1892–1940)

“A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
—Ralph Waldo Emerson (1803–1882)