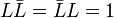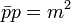Algebra of Physical Space - Special Relativity

Special Relativity

In APS, the space-time position is represented as a paravector

x = x^0 + x^1 \mathbf{e}_1 + x^2 \mathbf{e}_2 + x^3 \mathbf{e}_3,

where the time is given by the scalar part with . In the Pauli matrix representation the unit basis vectors are replaced by the Pauli matrices and the scalar part by the identity matrix. This means that the Pauli matrix representation of the space-time position is

x \rightarrow \begin{pmatrix} x^0 + x^3 && x^1 - ix^2 \\ x^1 + ix^2 && x^0-x^3 \end{pmatrix}

The four-velocity also called proper velocity is paravector defined as the proper time derivative of the space-time position

u = \frac{d x }{d \tau} = \frac{d x^0}{d\tau} + \frac{d}{d\tau}(x^1 \mathbf{e}_1 + x^2 \mathbf{e}_2 + x^3 \mathbf{e}_3) = \frac{d x^0}{d\tau}(1 + \frac{d}{d x^0}(x^1 \mathbf{e}_1 + x^2 \mathbf{e}_2 + x^3 \mathbf{e}_3)).

This expression can be brought to a more compact form by defining the ordinary velocity as

and recalling the definition of the gamma factor, so that the proper velocity becomes

u = \gamma(1+ \mathbf{v})

The proper velocity is a positive unimodular paravector, which implies the following condition in terms of the Clifford conjugation

u \bar{u} = 1

The proper velocity transforms under the action of the Lorentz rotor as

u \rightarrow u^\prime = L u L^\dagger.

The restricted Lorentz transformations that preserve the direction of time and include rotations and boosts can be performed by an exponentiation of the space-time rotation biparavector

L = e^{\frac{1}{2}W}

In the matrix representation the Lorentz rotor is seen to form an instance of the SL(2,C) group, which is the double cover of the Lorentz group. The unimodularity of the Lorentz rotor is translated in the following condition in terms of the product of the Lorentz rotor with its Clifford conjugation

L\bar{L} = \bar{L} L = 1

This Lorentz rotor can be always decomposed in two factors, one Hermitian, and the other unitary, such that

L = B R^{\,}

The unitary element is called rotor because encodes rotations and the Hermitian element is called boost.

The four-momentum in APS can be obtained by multiplying the proper velocity with the mass as

p = m u^{\,},

with the mass shell condition translated into

\bar{p}p = m^2

Read more about this topic:  Algebra Of Physical Space

Famous quotes containing the words special and/or relativity:

    “The very best reason parents are so special . . . is because we are the holders of a priceless gift, a gift we received from countless generations we never knew, a gift that only we now possess and only we can give to our children. That unique gift, of course, is the gift of ourselves. Whatever we can do to give that gift, and to help others receive it, is worth the challenge of all our human endeavor.”
    —Fred Rogers (20th century)

    “By an application of the theory of relativity to the taste of readers, to-day in Germany I am called a German man of science, and in England I am represented as a Swiss Jew. If I come to be regarded as a bête noire the descriptions will be reversed, and I shall become a Swiss Jew for the Germans and a German man of science for the English!”
    —Albert Einstein (1879–1955)