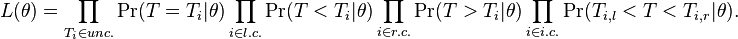Survival Analysis - Fitting Parameters To Data

Fitting Parameters To Data

Survival models can be usefully viewed as ordinary regression models in which the response variable is time. However, computing the likelihood function (needed for fitting parameters or making other kinds of inferences) is complicated by the censoring. The likelihood function for a survival model, in the presence of censored data, is formulated as follows. By definition the likelihood function is the conditional probability of the data given the parameters of the model. It is customary to assume that the data are independent given the parameters. Then the likelihood function is the product of the likelihood of each datum. It is convenient to partition the data into four categories: uncensored, left censored, right censored, and interval censored. These are denoted "unc.", "l.c.", "r.c.", and "i.c." in the equation below.

$L(\theta) = \prod_{T_i\in unc.} \Pr(T = T_i|\theta) \prod_{i\in l.c.} \Pr(T < T_i|\theta) \prod_{i\in r.c.} \Pr(T > T_i|\theta) \prod_{i\in i.c.} \Pr(T_{i,l} < T < T_{i,r}|\theta) .$

For an uncensored datum, with equal to the age at death, we have

For a left censored datum, such that the age at death is known to be less than, we have

For a right censored datum, such that the age at death is known to be greater than, we have

For an interval censored datum, such that the age at death is known to be less than and greater than, we have

$\Pr(T_{i,l} < T < T_{i,r}|\theta) = S(T_{i,l}|\theta) - S(T_{i,r}|\theta) .$

An important application where interval censored data arises is current status data, where the actual occurrence of an event is only known to the extent that it known not to occurred before observation time and to have occurred before the next.

Read more about this topic: Survival Analysis

Famous quotes containing the words fitting, parameters and/or data:

“The most fitting monuments this nation can build are schoolhouses and homes for those who do the work of the world. It is no answer to say that they are accustomed to rags and hunger. In this world of plenty every human being has a right to food, clothes, decent shelter, and the rudiments of education.”
—Elizabeth Cady Stanton (1815–1902)

“Men have defined the parameters of every subject. All feminist arguments, however radical in intent or consequence, are with or against assertions or premises implicit in the male system, which is made credible or authentic by the power of men to name.”
—Andrea Dworkin (b. 1946)

“This city is neither a jungle nor the moon.... In long shot: a cosmic smudge, a conglomerate of bleeding energies. Close up, it is a fairly legible printed circuit, a transistorized labyrinth of beastly tracks, a data bank for asthmatic voice-prints.”
—Susan Sontag (b. 1933)