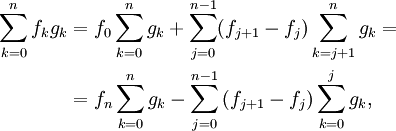Summation By Parts - Newton Series

Newton Series

The formula is sometimes given in one of these - slightly different - forms

$\begin{align}\sum_{k=0}^n f_k g_k &= f_0 \sum_{k=0}^n g_k+ \sum_{j=0}^{n-1} (f_{j+1}-f_j) \sum_{k=j+1}^n g_k=\\ &= f_n \sum_{k=0}^n g_k - \sum_{j=0}^{n-1} \left( f_{j+1}- f_j\right) \sum_{k=0}^j g_k, \end{align}$

which represent a special cases of the more general rule

$\begin{align}\sum_{k=0}^n f_k g_k &= \sum_{i=0}^{M-1} f_0^{(i)} G_{i}^{(i+1)}+ \sum_{j=0}^{n-M} f^{(M)}_{j} G_{j+M}^{(M)}=\\ &= \sum_{i=0}^{M-1} \left( -1 \right)^i f_{n-i}^{(i)} \tilde{G}_{n-i}^{(i+1)}+ \left( -1 \right) ^{M} \sum_{j=0}^{n-M} f_j^{(M)} \tilde{G}_j^{(M)};\end{align}$

both result from iterated application of the initial formula. The auxiliary quantities are Newton series:

and

A remarkable, particular result is the noteworthy identity

Here, is the binomial coefficient.

Read more about this topic: Summation By Parts

Famous quotes containing the words newton and/or series:

“The next Augustan age will dawn on the other side of the Atlantic. There will, perhaps, be a Thucydides at Boston, a Xenophon at New York, and, in time, a Virgil at Mexico, and a Newton at Peru. At last, some curious traveller from Lima will visit England and give a description of the ruins of St. Paul’s, like the editions of Balbec and Palmyra.”
—Horace Walpole (1717–1797)

“Autobiography is only to be trusted when it reveals something disgraceful. A man who gives a good account of himself is probably lying, since any life when viewed from the inside is simply a series of defeats.”
—George Orwell (1903–1950)