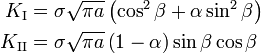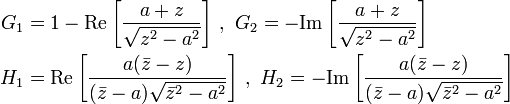Examples of Stress Intensity Factors
| Uniform uniaxial stress
The stress intensity factor for a through crack of length, at right angles, in an infinite plane, to a uniform stress field is If the crack is located centrally in a finite plate of width and height, an approximate relation for the stress intensity factor is If the crack is not located centrally along the width, i.e., the stress intensity factor at location A can be approximated by the series expansion where the factors can be found from fits to stress intensity curves for various values of . A similar (but not identical) expression can be found for tip B of the crack. Alternative expressions for the stress intensity factors at A and B are where with If the above expressions is the distance from the center of the crack to the boundary closest to point A. Note that when the above expressions do not simplify into the approximate expression for a centered crack. |
|
| Edge crack in a plate under uniaxial stress
For a plate of dimensions containing an edge crack of length, if the dimensions of the plate are such that and, the stress intensity factor at the crack tip under an uniaxial stress is For the situation where and, the stress intensity factor can be approximated by Specimens of this configuration are commonly used in fracture toughness testing. |
|
| Slanted crack in a biaxial stress field
For a slanted crack of length in a biaxial stress field with stress in the -direction and in the -direction, the stress intensity factors are where is the angle made by the crack with the -axis. |
|
| Penny-shaped crack in an infinite domain
The stress intensity factor at the tip of a penny-shaped crack of radius in an infinite domain under uniaxial tension is |
|
| Crack in a plate under point in-plane force
Consider a plate with dimensions containing a crack of length . A point force with components and is applied at the point of the plate. For the situation where the plate is large compared to the size of the crack and the location of the force is relatively close to the crack, i.e., the plate can be considered infinite. In that case, for the stress intensity factors for at crack tip B are where with, for plane strain, for plane stress, and is the Poisson's ratio. The stress intensity factors for at tip B are The stress intensity factors at the tip A can be determined from the above relations. For the load at location , Similarly for the load , |
|
| Loaded crack in a plate
If the crack is loaded by a point force located at and, the stress intensity factors at point B are If the force is distributed uniformly between, then the stress intensity factor at tip B is |
Read more about this topic: Stress Intensity Factor
Famous quotes containing the words examples of, examples, stress, intensity and/or factors:
“There are many examples of women that have excelled in learning, and even in war, but this is no reason we should bring ‘em all up to Latin and Greek or else military discipline, instead of needle-work and housewifry.”
—Bernard Mandeville (1670–1733)
“In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
—Michel de Montaigne (1533–1592)
“Like all weak men he laid an exaggerated stress on not changing one’s mind.”
—W. Somerset Maugham (1874–1966)
“Consider the difference between looking and staring. A look is voluntary; it is also mobile, rising and falling in intensity as its foci of interest are taken up and then exhausted. A stare has, essentially, the character of a compulsion; it is steady, unmodulated, “fixed.””
—Susan Sontag (b. 1933)
“I always knew I wanted to be somebody. I think that’s where it begins. People decide, “I want to be somebody. I want to make a contribution. I want to leave my mark here.” Then different factors contribute to how you will do that.”
—Faith Ringgold (b. 1934)


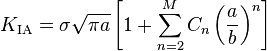

![\begin{align} \Phi_A &:= \left\sqrt{\sec\alpha_A} \\ \Phi_B &:= 1 + \left\right\}}\right] \end{align}](http://upload.wikimedia.org/math/c/0/6/c06cbe7cf169998103199d0347372019.png)

![K_{\rm I} = \sigma\sqrt{\pi a}\left[1.12 - 0.23\left(\frac{a}{b}\right) + 10.6\left(\frac{a}{b}\right)^2 - 21.7\left(\frac{a}{b}\right)^3 + 30.4\left(\frac{a}{b}\right)^4\right] \,.](http://upload.wikimedia.org/math/8/f/d/8fd245bef0e1536c3e224392a253d679.png)