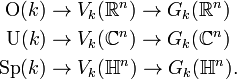Stiefel Manifold - As A Principal Bundle

As A Principal Bundle

There is a natural projection

from the Stiefel manifold Vk(Fn) to the Grassmannian of k-planes in Fn which sends a k-frame to the subspace spanned by that frame. The fiber over a given point P in Gk(Fn) is the set of all orthonormal k-frames contained in the space P.

This projection has the structure of a principal G-bundle where G is the associated classical group of degree k. Take the real case for concreteness. There is a natural right action of O(k) on Vk(Rn) which rotates a k-frame in the space it spans. This action is free but not transitive. The orbits of this action are precisely the orthonormal k-frames spanning a given k-dimensional subspace; that is, they are the fibers of the map p. Similar arguments hold in the complex and quaternionic cases.

We then have a sequence of principal bundles:

\begin{align} \mathrm O(k) &\to V_k(\mathbb R^n) \to G_k(\mathbb R^n)\\ \mathrm U(k) &\to V_k(\mathbb C^n) \to G_k(\mathbb C^n)\\ \mathrm{Sp}(k) &\to V_k(\mathbb H^n) \to G_k(\mathbb H^n). \end{align}

The vector bundles associated to these principal bundles via the natural action of G on Fk are just the tautological bundles over the Grassmannians. In other words, the Stiefel manifold Vk(Fn) is the orthogonal, unitary, or symplectic frame bundle associated to the tautological bundle on a Grassmannian.

When one passes to the n → ∞ limit, these bundles become the universal bundles for the classical groups.

Read more about this topic:  Stiefel Manifold

Famous quotes containing the words principal and/or bundle:

    “I would urge that the yeast of education is the idea of excellence, and the idea of excellence comprises as many forms as there are individuals, each of whom develops his own image of excellence. The school must have as one of its principal functions the nurturing of images of excellence.”
    —Jerome S. Bruner (20th century)

    ““There is Lowell, who’s striving Parnassus to climb
    With a whole bale of isms tied together with rhyme,
    He might get on alone, spite of brambles and boulders,
    But he can’t with that bundle he has on his shoulders,
    The top of the hill he will ne’er come nigh reaching
    Till he learns the distinction ‘twixt singing and preaching;”
    —James Russell Lowell (1819–1891)