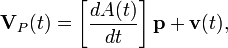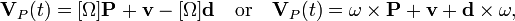Screw Theory - Twist

In order to define the twist of a rigid body, we must consider its movement defined by the parameterized set of spatial displacements, D(t)=(,d(f)), where is a rotation matrix and d is a translation vector. This causes a point p that is fixed in moving body to trace a curve P(t) in the fixed frame given by,

\mathbf{P}(t) = \mathbf{p} + \mathbf{d}(t).

The velocity of P is

\mathbf{V}_P(t) = \left\mathbf{p} + \mathbf{v}(t),

where v is velocity of the origin of the moving frame, that is dd/dt. Now substitute p= (P-d) into this equation to obtain,

\mathbf{V}_P(t) = \mathbf{P} + \mathbf{v} - \mathbf{d}\quad\mbox{or}\quad\mathbf{V}_P(t) = \mathbf{\omega}\times\mathbf{P} + \mathbf{v} + \mathbf{d}\times\mathbf{\omega},

where = is the angular velocity matrix and ω is the angular velocity vector.

The screw

is the twist of the moving body. The vector V=v + d×ω is the velocity of the point in the body that corresponds with the origin of the fixed frame.

There are two important special cases: (i) when d is constant, that is v=0, then the twist is a pure rotation about a line, then the twist is

and (ii) when =0, that is the body does not rotate but only slides in the direction v, then the twist is a pure slide given by

Read more about this topic:  Screw Theory

Famous quotes containing the word twist:

    “The duce of any other rule have I to govern myself by in this affair—and if I had one ... I would twist it and tear it to pieces, and throw it into the fire when I had done—Am I warm? I am, and the cause demands it—a pretty story! is a man to follow rules—or rules to follow him?”
    —Laurence Sterne (1713–1768)

    “For often at Church I’ve seen the stained high glass
    Pour out the Virgin and Saints, twist and untwist
    The mortal youth of Christ astride an ass.”
    —Allen Tate (1899–1979)

    “Talk to them about things they don’t know. Try to give them an inferiority complex. If the actress is beautiful, screw her. If she isn’t, present her with a valuable painting she will not understand. If they insist on being boring, kick their asses or twist their noses. And that’s about all there is to it.”
    —John Huston (1906–1987)