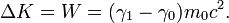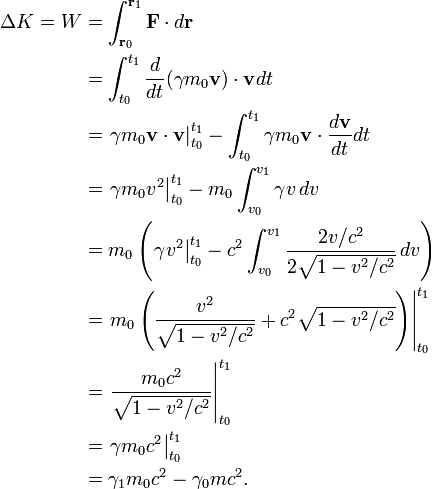Relativistic Mechanics - Kinetic Energy

Kinetic Energy

The work-energy theorem says the change in kinetic energy is equal to the work done on the body. In special relativity:

$\begin{align} \Delta K = W = (\gamma_1 - \gamma_0) m_0c^2.\end{align}$

Derivation
$\begin{align} \Delta K = W &= \int_{\mathbf{r}_0}^{\mathbf{r}_1} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{t_0}^{t_1} \frac{d}{dt}(\gamma m_0 \mathbf{v})\cdot\mathbf{v}dt \\ &= \left. \gamma m_0 \mathbf{v} \cdot \mathbf{v} \right\|^{t_1}_{t_0} - \int_{t_0}^{t_1} \gamma m_0\mathbf{v} \cdot \frac{d\mathbf{v}}{dt} dt \\ &= \left. \gamma m_0 v^2 \right\|^{t_1}_{t_0} - m_0\int_{v_0}^{v_1} \gamma v\,dv \\ &= m_0 \left( \left. \gamma v^2 \right\|^{t_1}_{t_0} - c^2\int_{v_0}^{v_1} \frac{2v/c^2}{2\sqrt{1-v^2/c^2}}\,dv \right) \\ &= \left. m_0\left(\frac {v^2}{\sqrt{1-v^2/c^2}} + c^2 \sqrt{1-v^2/c^2} \right) \right\|^{t_1}_{t_0} \\ &= \left. \frac {m_0c^2}{\sqrt{1-v^2/c^2}} \right\|^{t_1}_{t_0} \\ &= \left. {\gamma m_0c^2}\right\|^{t_1}_{t_0} \\ &= \gamma_1 m_0c^2 - \gamma_0 mc^2.\end{align}$

Derivation

$\begin{align} \Delta K = W &= \int_{\mathbf{r}_0}^{\mathbf{r}_1} \mathbf{F} \cdot d\mathbf{r} \\ &= \int_{t_0}^{t_1} \frac{d}{dt}(\gamma m_0 \mathbf{v})\cdot\mathbf{v}dt \\ &= \left. \gamma m_0 \mathbf{v} \cdot \mathbf{v} \right|^{t_1}_{t_0} - \int_{t_0}^{t_1} \gamma m_0\mathbf{v} \cdot \frac{d\mathbf{v}}{dt} dt \\ &= \left. \gamma m_0 v^2 \right|^{t_1}_{t_0} - m_0\int_{v_0}^{v_1} \gamma v\,dv \\ &= m_0 \left( \left. \gamma v^2 \right|^{t_1}_{t_0} - c^2\int_{v_0}^{v_1} \frac{2v/c^2}{2\sqrt{1-v^2/c^2}}\,dv \right) \\ &= \left. m_0\left(\frac {v^2}{\sqrt{1-v^2/c^2}} + c^2 \sqrt{1-v^2/c^2} \right) \right|^{t_1}_{t_0} \\ &= \left. \frac {m_0c^2}{\sqrt{1-v^2/c^2}} \right|^{t_1}_{t_0} \\ &= \left. {\gamma m_0c^2}\right|^{t_1}_{t_0} \\ &= \gamma_1 m_0c^2 - \gamma_0 mc^2.\end{align}$

If in the initial state the body was at rest (γ₀ = 1) and in the final state it has speed v (γ₁ = γ), the kinetic energy is

a result that can be directly obtained by subtracting the rest energy m₀c2 from the total relativistic energy γm₀c2.

Read more about this topic: Relativistic Mechanics

Famous quotes containing the words kinetic and/or energy:

“All my stories are webs of style and none seems at first blush to contain much kinetic matter.... For me “style” is matter.”
—Vladimir Nabokov (1899–1977)

“The welfare, the happiness, the energy and spirit of the men and women who do the daily work ... is the underlying necessity of all prosperity.... There can be nothing wholesome unless their life is wholesome; there can be no contentment unless they are contented.”
—Woodrow Wilson (1856–1924)

Related Phrases

Lorentz Transformation

Related Words