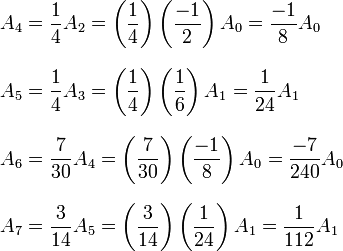Power Series Solution of Differential Equations - Example Usage

Example Usage

Let us look at the Hermite differential equation,

We can try to construct a series solution

Substituting these in the differential equation

\begin{align} & {} \quad \sum_{k=0}^\infty k(k-1)A_kz^{k-2}-2z\sum_{k=0}^\infty kA_kz^{k-1}+\sum_{k=0}^\infty A_kz^k=0 \\ & =\sum_{k=0}^\infty k(k-1)A_kz^{k-2}-\sum_{k=0}^\infty 2kA_kz^k+\sum_{k=0}^\infty A_kz^k \end{align}

Making a shift on the first sum

\begin{align} & = \sum_{k+2=0}^\infty (k+2)((k+2)-1)A_{k+2}z^{(k+2)-2}-\sum_{k=0}^\infty 2kA_kz^k+\sum_{k=0}^\infty A_kz^k \\ & =\sum_{k=-2}^\infty (k+2)(k+1)A_{k+2}z^k-\sum_{k=0}^\infty 2kA_kz^k+\sum_{k=0}^\infty A_kz^k \\ & =(0)(-1)A_0 z^{-2} + (1)(0)A_{1}z^{-1}+\sum_{k=0}^\infty (k+2)(k+1)A_{k+2}z^k-\sum_{k=0}^\infty 2kA_kz^k+\sum_{k=0}^\infty A_kz^k \\ & =\sum_{k=0}^\infty (k+2)(k+1)A_{k+2}z^k-\sum_{k=0}^\infty 2kA_kz^k+\sum_{k=0}^\infty A_kz^k \\ & =\sum_{k=0}^\infty \left((k+2)(k+1)A_{k+2}+(-2k+1)A_k\right)z^k \end{align}

If this series is a solution, then all these coefficients must be zero, so:

We can rearrange this to get a recurrence relation for Ak+2.

Now, we have

We can determine A0 and A1 if there are initial conditions, i.e. if we have an initial value problem.

So we have

\begin{align} A_4 & ={1\over 4}A_2 = \left({1\over 4}\right)\left({-1 \over 2}\right)A_0 = {-1 \over 8}A_0 \\ A_5 & ={1\over 4}A_3 = \left({1\over 4}\right)\left({1 \over 6}\right)A_1 = {1 \over 24}A_1 \\ A_6 & = {7\over 30}A_4 = \left({7\over 30}\right)\left({-1 \over 8}\right)A_0 = {-7 \over 240}A_0 \\ A_7 & = {3\over 14}A_5 = \left({3\over 14}\right)\left({1 \over 24}\right)A_1 = {1 \over 112}A_1 \end{align}

and the series solution is

\begin{align} f & = A_0x^0+A_1x^1+A_2x^2+A_3x^3+A_4x^4+A_5x^5+A_6x^6+A_7x^7+\cdots \\ & = A_0x^0 + A_1x^1 + {-1\over 2}A_0x^2 + {1\over 6}A_1x^3 + {-1 \over 8}A_0x^4 + {1 \over 24}A_1x^5 + {-7 \over 240}A_0x^6 + {1 \over 112}A_1x^7 + \cdots \\ & = A_0x^0 + {-1\over 2}A_0x^2 + {-1 \over 8}A_0x^4 + {-7 \over 240}A_0x^6 + A_1x + {1\over 6}A_1x^3 + {1 \over 24}A_1x^5 + {1 \over 112}A_1x^7 + \cdots \end{align}

which we can break up into the sum of two linearly independent series solutions:

which can be further simplified by the use of hypergeometric series.

Read more about this topic:  Power Series Solution Of Differential Equations

Famous quotes containing the word usage:

    “Pythagoras, Locke, Socrates—but pages
    Might be filled up, as vainly as before,
    With the sad usage of all sorts of sages,
    Who in his life-time, each was deemed a bore!
    The loftiest minds outrun their tardy ages.”
    —George Gordon Noel Byron (1788–1824)

    “Girls who put out are tramps. Girls who don’t are ladies. This is, however, a rather archaic usage of the word. Should one of you boys happen upon a girl who doesn’t put out, do not jump to the conclusion that you have found a lady. What you have probably found is a lesbian.”
    —Fran Lebowitz (b. 1951)