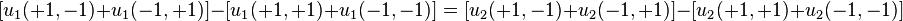Potential Game - A Simple Example

A Simple Example

	+1	–1
+1
–1
Fig. 1: Potential game example

In a 2-player, 2-strategy game with externalities, individual players' payoffs are given by the function u_i(s_i, s_j) = b_i s_i + w s_i s_j, where s_i is players i's strategy, s_j is the opponent's strategy, and w is a positive externality from choosing the same strategy. The strategy choices are +1 and −1, as seen in the payoff matrix in Figure 1.

This game has a potential function P(s₁, s₂) = b₁ s₁ + b₂ s₂ + w s₁ s₂.

If player 1 moves from −1 to +1, the payoff difference is Δu₁ = u₁(+1, s₂) – u₁(–1, s₂) = 2 b₁ + 2 w s₂.

The change in potential is ΔP = P(+1, s₂) – P(–1, s₂) = (b₁ + b₂ s₂ + w s₂) – (–b₁ + b₂ s₂ – w s₂) = 2 b₁ + 2 w s₂ = Δu₁.

The solution for player 2 is equivalent. Using numerical values b₁ = 2, b₂ = −1, w = 3, this example transforms into a simple battle of the sexes, as shown in Figure 2. The game has two pure Nash equilibria, (+1, +1) and (−1, −1). These are also the local maxima of the potential function (Figure 3). The only stochastically stable equilibrium is (+1, +1), the global maximum of the potential function.

	+1	–1
+1	5, 2	–1, –2
–1	–5, –4	1, 4
Fig. 2: Battle of the sexes (payoffs)

	+1	–1
+1	4	0
–1	–6	2
Fig. 3: Battle of the sexes (potentials)

A 2-player, 2-strategy game cannot be a potential game unless

$- = -$

Read more about this topic: Potential Game

Famous quotes containing the word simple:

“Even the simple act that we call “going to visit a person of our acquaintance” is in part an intellectual act. We fill the physical appearance of the person we see with all the notions we have about him, and in the totality of our impressions about him, these notions play the most important role.”
—Marcel Proust (1871–1922)