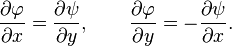Potential Flow - Analysis For Two-dimensional Flow

Analysis For Two-dimensional Flow

Potential flow in two dimensions is simple to analyze using conformal mapping, by the use of transformations of the complex plane. However, use of complex numbers is not required, as for example in the classical analysis of fluid flow past a cylinder. It is not possible to solve a potential flow using complex numbers in three dimensions.

The basic idea is to use a holomorphic (also called analytic) or meromorphic function f, which maps the physical domain (x,y) to the transformed domain (φ,ψ). While x, y, φ and ψ are all real valued, it is convenient to define the complex quantities

and

Now, if we write the mapping f as

or

Then, because f is a holomorphic or meromorphic function, it has to satisfy the Cauchy-Riemann equations

The velocity components (u,v), in the (x,y) directions respectively, can be obtained directly from f by differentiating with respect to z. That is

So the velocity field v = (u,v) is specified by

Both φ and ψ then satisfy Laplace's equation:

and

So φ can be identified as the velocity potential and ψ is called the stream function. Lines of constant ψ are known as streamlines and lines of constant φ are known as equipotential lines (see equipotential surface).

Streamlines and equipotential lines are orthogonal to each other, since

Thus the flow occurs along the lines of constant ψ and at right angles to the lines of constant φ.

It is interesting to note that Δψ = 0 is also satisfied, this relation being equivalent to ∇×v = 0. So the flow is irrotational. The automatic condition ∂2Ψ /( ∂x ∂y) = ∂2Ψ /( ∂y ∂x) then gives the incompressibility constraint ∇·v = 0.