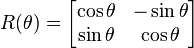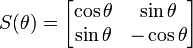Point Groups in Two Dimensions - More General Groups

More General Groups

These groups are readily constructed with two-dimensional orthogonal matrices.

The continuous cyclic group SO(2) or C_∞ and its subgroups have elements that are rotation matrices:

where SO(2) has any possible θ. Not surprisingly, SO(2) and its subgroups are all abelian; addition of rotation angles commutes.

For discrete cyclic groups C_n, elements C_nk = R(2πk/n)

The continuous dihedral group O(2) or D_∞ and its subgroups with reflections have elements that include not only rotation matrices, but also reflection matrices:

where O(2) has any possible θ. However, the only abelian subgroups of O(2) with reflections are D₁ and D₂.

For discrete dihedral groups D_n, elements C_nkσ = S(2πk/n)

When one uses polar coordinates, the relationship of these groups to one-dimensional symmetry groups becomes evident.

Types of subgroups of SO(2):

• finite cyclic subgroups C_n (n ≥ 1); for every n there is one isometry group, of abstract group type Z_n
• finitely generated groups, each isomorphic to one of the form Zm Z _n generated by C_n and m independent rotations with an irrational number of turns, and m, n ≥ 1; for each pair (m, n) there are uncountably many isometry groups, all the same as abstract group; for the pair (1, 1) the group is cyclic.
• other countable subgroups. For example, for an integer n, the group generated by all rotations of a number of turns equal to a negative integer power of n
• uncountable subgroups, including SO(2) itself

For every subgroup of SO(2) there is a corresponding uncountable class of subgroups of O(2) that are mutually isomorphic as abstract group: each of the subgroups in one class is generated by the first-mentioned subgroup and a single reflection in a line through the origin. These are the (generalized) dihedral groups, including the finite ones D_n (n ≥ 1) of abstract group type Dih_n. For n = 1 the common notation is C_s, of abstract group type Z₂.

As topological subgroups of O(2), only the finite isometry groups and SO(2) and O(2) are closed.

These groups fall into two distinct families, according to whether they consist of rotations only, or include reflections. The cyclic groups, C_n (abstract group type Z_n), consist of rotations by 360°/n, and all integer multiples. For example, a four legged stool has symmetry group C₄, consisting of rotations by 0°, 90°, 180°, and 270°. The symmetry group of a square belongs to the family of dihedral groups, D_n (abstract group type Dih_n), including as many reflections as rotations. The infinite rotational symmetry of the circle implies reflection symmetry as well, but formally the circle group S₁ is distinct from Dih(S₁) because the latter explicitly includes the reflections.

An infinite group need not be continuous; for example, we have a group of all integer multiples of rotation by 360°/√2, which does not include rotation by 180°. Depending on its application, homogeneity up to an arbitrarily fine level of detail in a transverse direction may be considered equivalent to full homogeneity in that direction, in which case these symmetry groups can be ignored.

C_n and D_n for n = 1, 2, 3, 4, and 6 can be combined with translational symmetry, sometimes in more than one way. Thus these 10 groups give rise to 17 wallpaper groups.