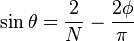Phased Array - Mathematical Perspective and Formulas

Mathematical Perspective and Formulas

A phased array is an example of N-slit diffraction. It may also be viewed as the coherent addition of N line sources. Since each individual antenna acts as a slit, emitting radio waves, their diffraction pattern can be calculated by adding the phase shift φ to the fringing term.

We will begin from the N-slit diffraction pattern derived on the diffraction formalism page.

\psi ={{\psi }_0}\left(\frac{\sin \left(\frac{{\pi a}}{\lambda }\sin\theta \right)}{\frac{{\pi a}}{\lambda }\sin\theta}\right)\left(\frac{\sin \left(\frac{N}{2}{kd}\sin\theta\right)}{\sin \left(\frac{{kd}}{2}\sin\theta \right)}\right)

Now, adding a φ term to the fringe effect in the second term yields:

\psi ={{\psi }_0}\left(\frac{\sin \left(\frac{{\pi a}}{\lambda }\sin \theta\right)}{\frac{{\pi a}}{\lambda }\sin\theta}\right)\left(\frac{\sin \left(\frac{N}{2}\big(\frac{{2\pi d}}{\lambda }\sin\theta + \phi \big)\right)}{\sin \left(\frac{{\pi d}}{\lambda }\sin\theta +\phi \right)}\right)

Taking the square of the wave function gives us the intensity of the wave.

I = I_0{{\left(\frac{\sin \left(\frac{\pi a}{\lambda }\sin\theta\right)}{\frac{{\pi a}}{\lambda } \sin \theta }\right)}^2}{{\left(\frac{\sin \left(\frac{N}{2}(\frac{2\pi d}{\lambda} \sin\theta+\phi )\right)}{\sin \left(\frac{{\pi d}}{\lambda } \sin\theta+\phi \right)}\right)}^2}
I =I_0{{\left(\frac{\sin \left(\frac{{\pi a}}{\lambda } \sin\theta\right)}{\frac{{\pi a}}{\lambda } \sin\theta}\right)}^2}{{\left(\frac{\sin \left(\frac{\pi }{\lambda } N d \sin\theta+\frac{N}{2} \phi \right)}{\sin \left(\frac{{\pi d}}{\lambda } \sin\theta+\phi \right)}\right)}^2}

Now space the emitters a distance apart. This distance is chosen for simplicity of calculation but can be adjusted as any scalar fraction of the wavelength.

I =I_0{{\left(\frac{\sin \left(\frac{\pi a}{\lambda } \sin\theta \right)}{\frac{\pi a}{\lambda } \sin\theta }\right)}^2}{{\left(\frac{\sin \left(\frac{\pi }{4} N \sin\theta+\frac{N}{2} \phi \right)}{\sin \left(\frac{\pi }{4} \sin\theta+ \phi \right)}\right)}^2}

As sine achieves its maximum at, we set the numerator of the second term = 1.

\frac{\pi }{4} N \sin\theta+\frac{N}{2} \phi = \frac{\pi }{2}
\sin\theta=\left(\frac{\pi }{2} - \frac{N}{2} \phi \right)\frac{4}{N \pi }
\sin\theta=\frac{2}{N}-\frac{2\phi }{\pi }

Thus as N gets large, the term will be dominated by the term. As sine can oscillate between −1 and 1, we can see that setting will send the maximum energy on an angle given by

Additionally, we can see that if we wish to adjust the angle at which the maximum energy is emitted, we need only to adjust the phase shift φ between successive antennas. Indeed the phase shift corresponds to the negative angle of maximum signal.

A similar calculation will show that the denominator is minimized by the same factor.

Read more about this topic:  Phased Array

Famous quotes containing the words mathematical, perspective and/or formulas:

    “The circumstances of human society are too complicated to be submitted to the rigour of mathematical calculation.”
    —Marquis De Custine (1790–1857)

    “No one thinks anything silly is suitable when they are an adolescent. Such an enormous share of their own behavior is silly that they lose all proper perspective on silliness, like a baker who is nauseated by the sight of his own eclairs. This provides another good argument for the emerging theory that the best use of cryogenics is to freeze all human beings when they are between the ages of twelve and nineteen.”
    —Anna Quindlen (20th century)

    “It is sentimentalism to assume that the teaching of life can always be fitted to the child’s interests, just as it is empty formalism to force the child to parrot the formulas of adult society. Interests can be created and stimulated.”
    —Jerome S. Bruner (20th century)