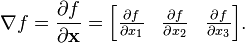Matrix Calculus - Scope

Scope

Matrix calculus refers to a number of different notations that use matrices and vectors to collect the derivative of each component of the dependent variable with respect to each component of the independent variable. In general, the independent variable can be a scalar, a vector, or a matrix while the dependent variable can be any of these as well. Each different situation will lead to a different set of rules, or a separate calculus, using the broader sense of the term. Matrix notation serves as a convenient way to collect the many derivatives in an organized way.

As a first example, consider the gradient from vector calculus. For a scalar function of three independent variables, the gradient is given by the vector equation

,

where represents a unit vector in the direction for . This type of generalized derivative can be seen as the derivative of a scalar, f, with respect to a vector, and its result can be easily collected in vector form.

\nabla f = \frac{\partial f}{\partial \mathbf{x}} = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} & \frac{\partial f}{\partial x_3} \\ \end{bmatrix}.

More complicated examples include the derivative of a scalar function with respect to a matrix, known as the gradient matrix, which collects the derivative with respect to each matrix element in the corresponding position in the resulting matrix. In that case the scalar must be a function of each of the independent variables in the matrix. As another example, if we have an n-vector of dependent variables, or functions, of m independent variables we might consider the derivative of the dependent vector with respect to the independent vector. The result could be collected in an m×n matrix consisting of all of the possible derivative combinations. There are, of course, a total of nine possibilities using scalars, vectors, and matrices. Notice that as we consider higher numbers of components in each of the independent and dependent variables we can be left with a very large number of possibilities.

The six kinds of derivatives that can be most neatly organized in matrix form are collected in the following table.

Types of Matrix Derivatives
Types Scalar Vector Matrix
Scalar
Vector
Matrix

Where we have used the term matrix in its most general sense, recognizing that vectors and scalars are simply matrices with one column and then one row respectively. Moreover, we have used bold letters to indicated vectors and bold capital letters for matrices. This notation is used throughout.

Notice that we could also talk about the derivative of a vector with respect to a matrix, or any of the other unfilled cells in our table. However, these derivatives are most naturally organized in a tensor of rank higher than 2, so that they do not fit neatly into a matrix. In the following three sections we will define each one of these derivatives and relate them to other branches of mathematics. See the layout conventions section for a more detailed table.

Read more about this topic:  Matrix Calculus

Famous quotes containing the word scope:

    “Revolutions are notorious for allowing even non- participants—even women!—new scope for telling the truth since they are themselves such massive moments of truth, moments of such massive participation.”
    —Selma James (b. 1930)

    “As the creative adult needs to toy with ideas, the child, to form his ideas, needs toys—and plenty of leisure and scope to play with them as he likes, and not just the way adults think proper. This is why he must be given this freedom for his play to be successful and truly serve him well.”
    —Bruno Bettelheim (20th century)

    “Happy is that mother whose ability to help her children continues on from babyhood and manhood into maturity. Blessed is the son who need not leave his mother at the threshold of the world’s activities, but may always and everywhere have her blessing and her help. Thrice blessed are the son and the mother between whom there exists an association not only physical and affectional, but spiritual and intellectual, and broad and wise as is the scope of each being.”
    —Lydia Hoyt Farmer (1842–1903)