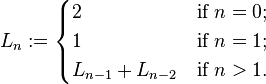Definition
Similarly to the Fibonacci numbers, each Lucas number is defined to be the sum of its two immediate previous terms, i.e. it is a Fibonacci integer sequence. However, the first two Lucas numbers are L0 = 2 and L1 = 1 instead of 0 and 1, and the properties of Lucas numbers are therefore somewhat different from those of Fibonacci numbers.
The Lucas numbers may thus be defined as follows:
The sequence of Lucas numbers begins:
- (sequence A000032 in OEIS).
All Fibonacci-like integer sequences appear in shifted form as a row of the Wythoff array; the Fibonacci sequence itself is the first row and the Lucas sequence is the second row. Also like all Fibonacci-like integer sequences, the ratio between two consecutive Lucas numbers converges to the golden ratio.
Read more about this topic: Lucas Number
Famous quotes containing the word definition:
“I’m beginning to think that the proper definition of “Man” is “an animal that writes letters.””
—Lewis Carroll [Charles Lutwidge Dodgson] (1832–1898)
“Was man made stupid to see his own stupidity?
Is God by definition indifferent, beyond us all?
Is the eternal truth man’s fighting soul
Wherein the Beast ravens in its own avidity?”
—Richard Eberhart (b. 1904)
“Beauty, like all other qualities presented to human experience, is relative; and the definition of it becomes unmeaning and useless in proportion to its abstractness. To define beauty not in the most abstract, but in the most concrete terms possible, not to find a universal formula for it, but the formula which expresses most adequately this or that special manifestation of it, is the aim of the true student of aesthetics.”
—Walter Pater (1839–1894)