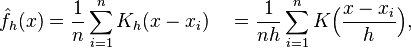Kernel Density Estimation - Definition

Definition

Let (x1, x2, …, xn) be an iid sample drawn from some distribution with an unknown density ƒ. We are interested in estimating the shape of this function ƒ. Its kernel density estimator is

\hat{f}_h(x) = \frac{1}{n}\sum_{i=1}^n K_h (x - x_i) \quad = \frac{1}{nh} \sum_{i=1}^n K\Big(\frac{x-x_i}{h}\Big),

where K(•) is the kernel — a symmetric but not necessarily positive function that integrates to one — and h > 0 is a smoothing parameter called the bandwidth. A kernel with subscript h is called the scaled kernel and defined as Kh(x) = 1/h K(x/h). Intuitively one wants to choose h as small as the data allow, however there is always a trade-off between the bias of the estimator and its variance; more on the choice of bandwidth later.

A range of kernel functions are commonly used: uniform, triangular, biweight, triweight, Epanechnikov, normal, and others. The Epanechnikov kernel is optimal in a minimum variance sense, though the loss of efficiency is small for the kernels listed previously, and due to its convenient mathematical properties, the normal kernel is often used K(x) = ϕ(x), where ϕ is the standard normal density function.

The construction of a kernel density estimate finds interpretations in fields outside of density estimation. For example, in thermodynamics, this is equivalent to the amount of heat generated when heat kernels (the fundamental solution to the heat equation) are placed at each data point locations xi. Similar methods are used to construct discrete Laplace operators on point clouds for manifold learning.

Read more about this topic:  Kernel Density Estimation

Famous quotes containing the word definition:

    “Although there is no universal agreement as to a definition of life, its biological manifestations are generally considered to be organization, metabolism, growth, irritability, adaptation, and reproduction.”
    —The Columbia Encyclopedia, Fifth Edition, the first sentence of the article on “life” (based on wording in the First Edition, 1935)

    “The very definition of the real becomes: that of which it is possible to give an equivalent reproduction.... The real is not only what can be reproduced, but that which is always already reproduced. The hyperreal.”
    —Jean Baudrillard (b. 1929)

    “Was man made stupid to see his own stupidity?
    Is God by definition indifferent, beyond us all?
    Is the eternal truth man’s fighting soul
    Wherein the Beast ravens in its own avidity?”
    —Richard Eberhart (b. 1904)