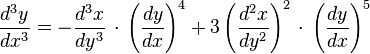Inverse Functions and Differentiation - Higher Derivatives

Higher Derivatives

The chain rule given above is obtained by differentiating the identity x = f −1(f(x)) with respect to x. One can continue the same process for higher derivatives. Differentiating the identity with respect to x two times, one obtains

or replacing the first derivative using the formula above,

.

Similarly for the third derivative:

\frac{d^3y}{dx^3} = - \frac{d^3x}{dy^3}\,\cdot\,\left(\frac{dy}{dx}\right)^4 - 3 \frac{d^2x}{dy^2}\,\cdot\,\frac{d^2y}{dx^2}\,\cdot\,\left(\frac{dy}{dx}\right)^2

or using the formula for the second derivative,

\frac{d^3y}{dx^3} = - \frac{d^3x}{dy^3}\,\cdot\,\left(\frac{dy}{dx}\right)^4 + 3 \left(\frac{d^2x}{dy^2}\right)^2\,\cdot\,\left(\frac{dy}{dx}\right)^5

These formulas are generalized by the Faà di Bruno's formula.

These formulas can also be written using Lagrange's notation. If f and g are inverses, then

Read more about this topic:  Inverse Functions And Differentiation

Famous quotes containing the word higher:

    “Dreams have a poetic integrity and truth. This limbo and dust- hole of thought is presided over by a certain reason, too. Their extravagance from nature is yet within a higher nature.”
    —Ralph Waldo Emerson (1803–1882)