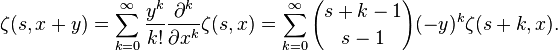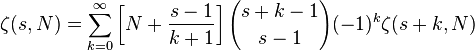Taylor Series
The derivative of the zeta in the second argument is a shift:
Thus, the Taylor series has the distinctly umbral form:
Closely related is the Stark–Keiper formula:
which holds for integer N and arbitrary s. See also Faulhaber's formula for a similar relation on finite sums of powers of integers.
Read more about this topic: Hurwitz Zeta Function
Famous quotes containing the words taylor and/or series:
“Once at thy Feast, I saw thee Pearle-like stand
‘Tween Heaven and Earth, where Heavens Bright glory all
In streams fell on thee, as a floodgate and
Like Sun Beams through thee on the World to Fall.
Oh! Sugar sweet then! My Deare sweet Lord, I see
Saints Heaven-lost Happiness restor’d by thee.”
—Edward Taylor (1645–1729)
“Every Age has its own peculiar faith.... Any attempt to translate into facts the mission of one Age with the machinery of another, can only end in an indefinite series of abortive efforts. Defeated by the utter want of proportion between the means and the end, such attempts might produce martyrs, but never lead to victory.”
—Giuseppe Mazzini (1805–1872)