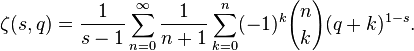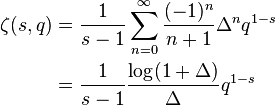Hurwitz Zeta Function - Series Representation

Series Representation

A convergent series representation defined for q > −1 and any complex s ≠ 1 was given by Helmut Hasse in 1930:

\zeta(s,q)=\frac{1}{s-1} \sum_{n=0}^\infty \frac{1}{n+1} \sum_{k=0}^n (-1)^k {n \choose k} (q+k)^{1-s}.

This series converges uniformly on compact subsets of the s-plane to an entire function. The inner sum may be understood to be the nth forward difference of ; that is,

where Δ is the forward difference operator. Thus, one may write

\begin{align} \zeta(s, q) &= \frac{1}{s-1}\sum_{n=0}^\infty \frac{(-1)^n}{n+1} \Delta^n q^{1-s}\\ &= \frac{1}{s-1} {\log(1 + \Delta) \over \Delta} q^{1-s} \end{align}

Read more about this topic:  Hurwitz Zeta Function

Famous quotes containing the word series:

    “Life ... is not simply a series of exciting new ventures. The future is not always a whole new ball game. There tends to be unfinished business. One trails all sorts of things around with one, things that simply won’t be got rid of.”
    —Anita Brookner (b. 1928)