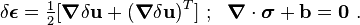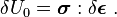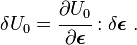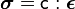Thermodynamic Basis
Linear deformations of elastic materials can be approximated as adiabatic. Under these conditions and for quasistatic processes the first law of thermodynamics for a deformed body can be expressed as
where is the increase in internal energy and is the work done by external forces. The work can be split into two terms
where is the work done by surface forces while is the work done by body forces. If is a variation of the displacement field in the body, then the two external work terms can be expressed as
where is the surface traction vector, is the body force vector, represents the body and represents its surface. Using the relation between the Cauchy stress and the surface traction, (where is the unit outward normal to ), we have
Converting the surface integral into a volume integral via the divergence theorem gives
Using the symmetry of the Cauchy stress and the identity
we have
From the definition of strain and from the equations of equilibrium we have
Hence we can write
and therefore the variation in the internal energy density is given by
An elastic material is defined as one in which the total internal energy is equal to the potential energy of the internal forces (also called the elastic strain energy). Therefore the internal energy density is a function of the strains, and the variation of the internal energy can be expressed as
Since the variation of strain is arbitrary, the stress-strain relation of an elastic material is given by
For a linear elastic material, the quantity is a linear function of, and can therefore be expressed as
where is a fourth-rank tensor of material constants, also called the stiffness tensor. We can see why must be a fourth-rank tensor by noting that, for a linear elastic material,
In index notation
Clearly, the right hand side constant requires four indices and is a fourth-rank quantity. We can also see that this quantity must be a tensor because it is a linear transformation that takes the strain tensor to the stress tensor. We can also show that the constant obeys the tensor transformation rules for fourth rank tensors.
Read more about this topic: Hooke's Law
Famous quotes containing the word basis:
“This seems to be advanced as the surest basis for our belief in the existence of gods, that there is no race so uncivilized, no one in the world so barbarous that his mind has no inkling of a belief in gods.”
—Marcus Tullius Cicero (106–43 B.C.)
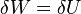




![\boldsymbol{\nabla}\cdot(\boldsymbol{A}\cdot\mathbf{b}) = (\boldsymbol{\nabla}\cdot\boldsymbol{A})\cdot\mathbf{b}+
\tfrac{1}{2}[\boldsymbol{A}^T:\boldsymbol{\nabla}\mathbf{b}+ \boldsymbol{A}:(\boldsymbol{\nabla}\mathbf{b})^T]](http://upload.wikimedia.org/math/5/2/e/52ef8bb5ab9839a43ab4b38786a70de3.png)
![\delta U = \int_{\Omega} [\boldsymbol{\sigma}:
\tfrac{1}{2}\{\boldsymbol{\nabla}\delta\mathbf{u}+(\boldsymbol{\nabla}\delta\mathbf{u})^T\} + \{\boldsymbol{\nabla}\cdot\boldsymbol{\sigma}+\mathbf{b}\}\cdot\delta\mathbf{u}]~{\rm dV} ~.](http://upload.wikimedia.org/math/b/f/f/bff1b7f2816fe38684e9682703cf0dac.png)