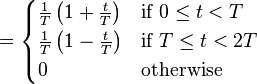Lastly, the predictive first-order hold is quite different. This is a causal hypothetical LTI system or filter that converts the ideally sampled signal
into a piecewise linear output such that the current sample and immediately previous sample are used to linearly extrapolate up to the next sampling instance. The output of such a filter would be
resulting in an effective impulse response of
- where is the rectangular function and is the triangular function.
The effective frequency response is the continuous Fourier transform of the impulse response.
- where is the sinc function.
The Laplace transform transfer function of the predictive FOH is found by substituting s = i 2 π f:
This a causal system. The impulse response of the predictive FOH does not respond before the input impulse.
This kind of piecewise linear reconstruction is physically realizable by implementing a digital filter of gain H(z) = 1 − z−1, applying the output of that digital filter (which is simply x−x) to an ideal conventional digital-to-analog converter (that has an inherent zero-order hold as its model) and applying that DAC output to an analog filter with transfer function H(s) = (1+sT)/(sT).
Read more about this topic: First-order Hold
Famous quotes containing the word hold:
“There’s something like a line of gold thread running through a man’s words when he talks to his daughter, and gradually over the years it gets to be long enough for you pick up in your hands and weave into a cloth that feels like love itself. It’s another thing, though, to hold up that cloth for inspection.”
—John Gregory Brown (20th century)