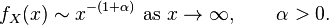Fat-tailed Distribution - Definition

Definition

The distribution of a random variable X is said to have a fat tail if

\Pr \sim x^{- \alpha}\text{ as }x \to \infty,\qquad \alpha > 0.\,

That is, if X has a probability density function, ,

f_X(x) \sim x^{ - (1 + \alpha)} \text{ as }x \to \infty, \qquad \alpha > 0.\,

Here the notation "" is the "twiddles" notation used for the asymptotic equivalence of functions. Some reserve the term "fat tail" for distributions only where 0 < α < 2 (i.e. only in cases with infinite variance).

Read more about this topic:  Fat-tailed Distribution

Famous quotes containing the word definition:

    “Perhaps the best definition of progress would be the continuing efforts of men and women to narrow the gap between the convenience of the powers that be and the unwritten charter.”
    —Nadine Gordimer (b. 1923)

    “One definition of man is “an intelligence served by organs.””
    —Ralph Waldo Emerson (1803–1882)

    “The definition of good prose is proper words in their proper places; of good verse, the most proper words in their proper places. The propriety is in either case relative. The words in prose ought to express the intended meaning, and no more; if they attract attention to themselves, it is, in general, a fault.”
    —Samuel Taylor Coleridge (1772–1834)