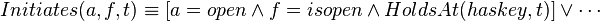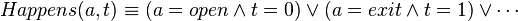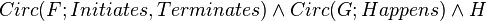Domain-dependent Axioms
The axioms above relate the value of the predicates, and, but do not specify which fluents are known to be true and which actions actually make fluents true or false. This is done by using a set of domain-dependent axioms. The known values of fluents are stated as simple literals . The effects of actions are stated by formulae relating the effects of actions with their preconditions. For example, if the action makes the fluent true, but only if is currently true, the corresponding formula in the event calculus is:
The right-hand expression of this equivalence is composed of a disjunction: for each action and fluent that can be made true by the action, there is a disjunct saying that is actually that action, that is actually that fluent, and that the precondition of the action is met.
The formula above specifies the truth value of for every possible action and fluent. As a result, all effects of all actions have to be combined in a single formulae. This is a problem, because the addition of a new action requires modifying an existing formula rather than adding new ones. This problem can be solved by the application of circumscription to a set of formulae each specifying one effect of one action:
These formulae are simpler than the formula above, because each effect of each action can be specified separately. The single formula telling which actions and fluents make true has been replaced by a set of smaller formulae, each one telling the effect of an action to a fluent.
However, these formulae are not equivalent to the formula above. Indeed, they only specify sufficient conditions for to be true, which should be completed by the fact that is false in all other cases. This fact can be formalized by simply circumscribing the predicate in the formula above. It is important to note that this circumscription is done only on the formulae specifying and not on the domain-independent axioms. The predicate can be specified in the same way is.
A similar approach can be taken for the predicate. The evaluation of this predicate can be enforced by formulae specifying not only when it is true and when it is false:
Circumscription can simplify this specification, as only necessary conditions can be specified:
Circumscribing the predicate, this predicate will be false in all points in which it is not explicitly specified to be true. This circumscription has to be done separately from the circumscription of the other formulae. In other words, if is the set of formulae of the kind, is the set of formulae, and are the domain independent axioms, the correct formulation of the domain is:
Read more about this topic: Event Calculus
Famous quotes containing the word axioms:
“The axioms of physics translate the laws of ethics. Thus, “the whole is greater than its part;” “reaction is equal to action;” “the smallest weight may be made to lift the greatest, the difference of weight being compensated by time;” and many the like propositions, which have an ethical as well as physical sense. These propositions have a much more extensive and universal sense when applied to human life, than when confined to technical use.”
—Ralph Waldo Emerson (1803–1882)