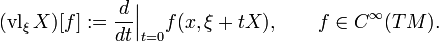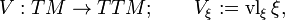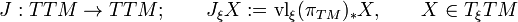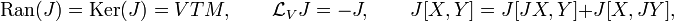Double Tangent Bundle - Canonical Tensor Fields On The Tangent Bundle

Canonical Tensor Fields On The Tangent Bundle

As for any vector bundle, the tangent spaces T_ξ(T_xM) of the fibres T_xM of the tangent bundle (TM,π_TM,M) can be identified with the fibres T_xM themselves. Formally this is achieved though the vertical lift, which is a natural vector space isomorphism vl_ξ:T_xM→V_ξ(T_xM) defined as

$(\operatorname{vl}_\xi X):=\frac{d}{dt}\Big|_{t=0}f(x,\xi+tX), \qquad f\in C^\infty(TM).$

The vertical lift can also be seen as a natural vector bundle isomorphism vl:(π_TM)*TM→VTM from the pullback bundle of (TM,π_TM,M) over π_TM:TM→M onto the vertical tangent bundle

$VTM:=\operatorname{Ker}(\pi_{TM})_* \subset TTM.$

The vertical lift lets us define the canonical vector field

$V:TM\to TTM; \qquad V_\xi := \operatorname{vl}_\xi\xi,$

which is smooth in the slit tangent bundle TM\0. The canonical vector field can be also defined as the infinitesimal generator of the Lie-group action

$\mathbb R\times (TM\setminus 0) \to TM\setminus 0; \qquad (t,\xi) \mapsto e^t\xi.$

Unlike the canonical vector field, which can be defined for any vector bundle, the canonical endomorphism

$J:TTM\to TTM; \qquad J_\xi X := \operatorname{vl}_\xi(\pi_{TM})_*X, \qquad X\in T_\xi TM$

is special to the tangent bundle. The canonical endomorphism J satisfies

$\operatorname{Ran}(J)=\operatorname{Ker}(J)=VTM, \qquad \mathcal L_VJ= -J, \qquad J=J+J,$

and it is also known as the tangent structure for the following reason. If (E,p,M) is any vector bundle with the canonical vector field V and a (1,1)-tensor field J that satisfies the properties listed above, with VE in place of VTM, then the vector bundle (E,p,M) is isomorphic to the tangent bundle (TM,π_TM,M) of the base manifold, and J corresponds to the tangent structure of TM in this isomorphism.

There is also a stronger result of this kind which states that if N is a 2n-dimensional manifold and if there exists a (1,1)-tensor field J on N that satisfies

$\operatorname{Ran}(J)=\operatorname{Ker}(J), \qquad J=J+J,$

then N is diffeomorphic to an open set of the total space of a tangent bundle of some n-dimensional manifold M, and J corresponds to the tangent structure of TM in this diffeomorphism.

In any associated coordinate system on TM the canonical vector field and the canonical endomorphism have the coordinate representations

$V = \xi^k\frac{\partial}{\partial \xi^k}, \qquad J = dx^k\otimes\frac{\partial}{\partial \xi^k}.$

Read more about this topic: Double Tangent Bundle

Famous quotes containing the words canonical, fields and/or bundle:

“If God bestowed immortality on every man then when he made him, and he made many to whom he never purposed to give his saving grace, what did his Lordship think that God gave any man immortality with purpose only to make him capable of immortal torments? It is a hard saying, and I think cannot piously be believed. I am sure it can never be proved by the canonical Scripture.”
—Thomas Hobbes (1579–1688)

“What doubts, what hypotheses, what labyrinths of amusement, what fields of disputation, what an ocean of false learning, may be avoided by that single notion of immaterialism!”
—George Berkeley (1685–1753)

“We styled ourselves the Knights of the Umbrella and the Bundle; for, wherever we went ... the umbrella and the bundle went with us; for we wished to be ready to digress at any moment. We made it our home nowhere in particular, but everywhere where our umbrella and bundle were.”
—Henry David Thoreau (1817–1862)